Canary: Practical Static Detection of Inter-thread Value-Flow Bugs 论文阅读笔记
2 Canary in a Nutshell
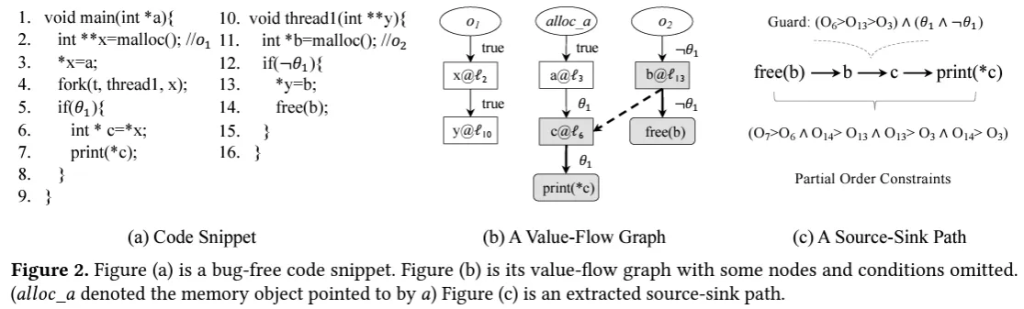
线程内部的数值流图(Intra-thread Value-Flow Graph)
$o_1$对象的指针为:$x\text{@}l_2 \rightarrow y\text{@}l_{10}$ 其中$y\text{@}l_{10}$为函数$\text{thread1}$的形式参数
$a$所指的对象的指针为:$a\text{@}l_3\rightarrow c\text{@}l_6\rightarrow \text{print(*c)}$
$o_2$对象的指针为:$b\text{@}l_3\rightarrow\text{free(b)}$
Guard of Edge from $b\text{@}l_3$ to $c\text{@}l_6$ is
- Under which the value flows through the same memory object $o_1$
- Enforcing that the value loaded from a load statement($l_6$) is the value stored by the most recent store statement($l_{13}$)
数值流(Value Flow)
变量$𝑎$的值流向变量$𝑏$,如果$𝑎$被直接(通过赋值,例如 $𝑏=𝑎$)或间接(通过指针引用,例如$∗𝑦=𝑎;𝑥= 𝑦;𝑏=∗𝑥$)地赋值给$𝑏$。$𝑎$和$𝑏$之间的关系可以是Data Dependence或Interference Dependence取决于值流是否跨越线程发生。值流图可以被定义为有向图。每个节点$𝑛$用$𝑣@ℓ$ 表示,表示变量$𝑣$在程序位置 $ℓ$被定义或使用。表示值流关系的边可以表示为元组$(𝑣_1\text{@}ℓ_1,𝑣_2\text{@}ℓ_2)$。注解的$Φ𝑔𝑢𝑎𝑟𝑑$表示值流发生的条件。值流图上的路径$\pi=⟨𝑣_1\text{@}ℓ_1,…,𝑣_𝑛\text{@}ℓ_𝑛⟩$被称为值流路径。
在编译器设计中,静态单赋值(Static Single assignment,SSA)形式是中间表示(Intermediate Representation,IR)的一个特性,要求每个变量只能被赋值一次,且使用之前必须被定义。原IR 中现有变量被分割成版本,通常在教科书中使用原始名称加下标表示新的变量版本。 Partial SSA: – Top-level variables are in SSA from – Address-taken variables are not
基于Partial SSA形式的语句可以较容易地识别直接流。因此,重点放在通过Data Dependence, Interference Dependence从Store语句到Load语句的间接流上,这需要对指针信息进行推理.
4种类型指针操作(Four-typed Pointer Operations)
- ALLOC:$p=allo\_o$
- ASSIGN:$p = q$
- STORE:$*x = q$(将变量$q$的值存放在指针$x$所指的位置)
- LOAD:$p = *y$ (将指针$x$所指位置的值加载到变量$q$中)
4. Thread-Modular Dependence Analysis
逆后序遍历(Reverse Postorder Traversal)
A postorder traversal visits as many of a node’s children as possible, in a consistent order, before visiting the node. (In a cyclic graph, a node’s child may also be its ancestor).
An reverse postorder(RPO) traversal is the opposite – it visits as many of a node’s predecessors as possible before visiting the node itself.
What is the reverse postorder?
Intra-thread数据依赖(Data Dependence)
- Intra-procedural Analysis
在HandleEachInst(I)中,分别处理4种指针操作[$PG_{top}$表示Top-level的Points-to Graph]:

- $l,\phi:p=allo\_o$
条件$\phi$下,语句$l$中,$p$指向o,即$PG_{top}\hookleftarrow\{p\mapsto(\phi,alloc_o)\}$
- $l,\phi:p=q$
条件$\phi$下,语句$l$中,$p$指向o,当条件$\gamma$下,$q$指向o,即
$PG_{top}\hookleftarrow\{p\mapsto(\gamma\wedge\phi,alloc_o)\},\forall(\gamma,o)\in Pts(q);$
- Inter-procedural Analysis
干扰依赖(Inteference Dependence)
- Interference Dependence Analysis
- Dependence Edges Computation
- Dependence Guard Computation
