社区发现 (Community Detection)
最大流/最小割(Max-flow Min-cut)
In the minimum-cut method, the network is divided into a predetermined number of parts, usually of approximately the same size, chosen such that the number of edges between groups is minimized.
Community structure – Wikipedia
层次聚类(Hierarchical clustering)
凝聚(Agglomerative)
自下而上的方式工作。首先将每个对象作为单独的一个原子簇,然后合并这些原子簇形成越来越大的簇,直到所有的对象都在一个簇中,或者达到某个终止条件。绝大多数层次聚类方法属于这一类。
其中一个重要的步骤是如何确定停止凝聚聚类的阈值,以接近最优的社区结构。
分裂(Diverse)
自顶向下的方式工作。首先将所有对象置于一个簇中,然后逐渐细分为越来越小的簇,直到每一个对象自成一个簇,或者达到某个终止条件;例如达到了某个希望的簇的数目,或者两个最近的簇之间的距离超过了某个阈值。
层次聚类算法_Jason__T的博客-CSDN博客_层次聚类算法
簇(Cluster)间距离计算
最短(Minimum)距离
单链接聚类(Single-linkage clustering)算法通常使用最短距离:当且仅当不同簇中的所有节点对的相似性低于给定阈值时,两个组才被认为是独立的社区。
Single-linkage clustering – Wikipedia
最长(Maximum)距离
全链接聚类(Complete-linkage clustering)或称最远邻居聚类(Farthest neighbour clustering)算法通常使用最长距离:当且仅当不同簇中的所有节点对的相似性高于给定阈值时,两个组才被认为是独立的社区。
Complete-linkage clustering – Wikipedia
Girvan–Newman算法
介数中心性(Betweenness Centrality)
$$ g(v)=\sum_{s\neq v\neq t}{\sigma_{st}{(v)}\over \sigma_{st}} $$
$\sigma_{st}$ 表示节点 $s$ 到节点 $t$ 到最短路径的数量,$\sigma_{st}(v)$ 表示这些路径经过 $v$ 的次数。
边介数(Edge Betweenness)
Girvan–Newman将弗里曼的介数中心性(Freeman’s betweenness centrality)推广到边,并将边的边介数定义为经过此边的最短路径的数量。
算法过程
Girvan-Newman algorithm – Wikipedia
- The betweenness of all existing edges in the network is calculated first.
- The edge(s) with the highest betweenness are removed.
- The betweenness of all edges affected by the removal is recalculated.
- Steps 2 and 3 are repeated until no edges remain.
Girvan–Newman算法的最终结果是树状图(dendrogram)。树状图随着算法的运行自上而下生成的,即网络分裂成不同的社区,并持续删除链接。树状图的叶子是单独的网络节点。
算法复杂度
计算包含 $n$ 个节点图中的 $m$ 条边的边介数所需的时间为 $O(mn)$. 因为每去除一条边计算必须重复一次,因此算法运行的最坏的时间复杂度为 $O(m^2n)$. 然而,在删除每条边之后,我们只需要重新计算那些受删除影响的边的介数,最多只是与删除的边在同一组(component)中的那些边。
基于模块度的方法(Modularity Maximation)
定义一种收益函数用于衡量将网络划分为社区的质量,也就是模块度(Modularity)。基于模块度的方法通过在网络的可能划分中搜索一个或多个具有特别高模块化的划分来进行社区检测,通常基于近似最优化方法(Approximate Optimization Methods), 例如贪婪算法、模拟退火或谱优化,使用不同的方法在速度和精度之间提供不同的平衡;一种流行的方法是Louvain方法。
模块度
Modularity (networks) – Wikipedia
Modularity is the fraction of the edges that fall within the given groups minus the expected fraction if edges were distributed at random.
对于带权图(weighted graph),Louvain方法中使用的模块度定义为:
$$ Q= {1\over 2m} \sum_{ij}{[A_{ij}-{k_ik_j \over 2m}] \delta (c_i,c_j)} $$
- $A_{ij}$ 表示图中节点 $i$ 和 $j$ 之间的边的权重,如果节点 $i$ 和 $j$ 之间没有边,则 $A_{ij} = 0$
- $k_i$ 和 $k_j$ 分别表示连接节点 $i$ 和 $j$ 的边的权重之和;即$k_i = \sum_j{A_{ij}}$, $k_j = \sum_i{A_{ij}}$
- $m$ 表示图中的所有边的权重的累加和;即 $m={1\over 2} \sum_{ij}A_{ij}$
- $c_i$ 和 $c_j$分别表示节点 $i$ 和 $j$ 所在的社区
- $\delta$ 是 Kronecker delta 函数;$\delta(x,y)$ 当 x 等于 y 时返回1,否则返回0
公式可以知道,累加的节点 $i$ 和 $j$ 对是位于同一个社区内的;因此,对于社区 c 的模块度:
$$ Q_c= {1\over 2m} \sum_{ij}{[A_{ij}-{k_ik_j \over 2m}]} = {\sum_{ij}A_{ij} \over 2m} – ({\sum_{i}{k_i} \over 2m})^2 = {\sum_{in} \over 2m} – ({\sum_{tot} \over 2m})^2 $$
- 节点 $i$ 和 $j$ 都是位于社区 c 内的节点
- $\sum_{in}$ 表示社区内节点之间的边权重之和(每条边被考虑了2次)
- $\sum_{tot}$ 表示社区内节点之间的边权重之和(每条边被考虑了2次),外加上连接该社区与其他社区的边权重之和(这些边只被考虑了1次)
因此对每个社区 c 累加,模块度公式也有:
$$ Q = \sum_cQ_c = \sum_c[{{\sum_{in} \over 2m} – ({\sum_{tot} \over 2m})^2}] $$
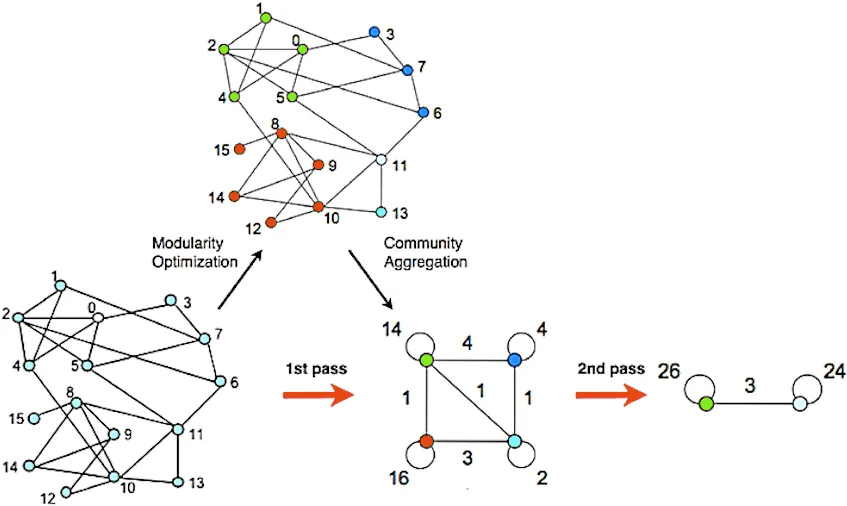
Louvain方法
Fast unfolding of communities in large networks
算法过程
Louvain算法的每轮迭代有两个阶段:
- 初始,网络中的每个节点自成一个社区。然后对于每个节点 $i$,将 $i$ 从其原来的社区中删除并添加到某个它的邻居节点 $j$ 所在社区,以使此过程的模块度变化量 $\Delta Q$ 最大;如果节点 $i$ 迁移到任何邻居节点的社区产生的 $\Delta Q$ 都不是正数,那么将节点 $i$ 保持在原来的社区中。持续迭代过程直到所有的节点都无法因为单次迁移获得正值模块度变化量,第一阶段结束。
Once this local maximum of modularity is hit, the first phase has ended.
- 将第一阶段获得的每个社区聚合为一个新节点。然后将原来位于社区内部的边聚合成新节点的带权环,原来位于社区之间边聚合成新节点间带权的边。最后将聚合后的图作为下一轮迭代的第一阶段的输入。
基于统计推断的方法(Statistical Inference)
Statistical inference – Wikipedia
统计推断(statistical inference)是指根据带随机性的观测数据(样本)以及问题的条件和假(模型)来对未知事物作出的、以概率形式表述的推断。
生成模型(Generative Model)的定义与判别模型(Discriminative Model)相对应:生成模型是所有变量的全概率模型,而判别模型是在给定观测变量值前提下目标变量条件概率模型。因此生成模型能够用于模拟/生成模型中任意变量的分布情况,而判别模型只能根据观测变量得到目标变量的采样。判别模型不对观测变量的分布建模,因此它不能够表达观测变量与目标变量之间更复杂的关系。因此,生成模型更适用于无监督的任务,如分类和聚类。
- [ ] 学习《概率论与数理统计》相关知识,进一步调研基于统计推断的社区发现方法