博弈论(研究生课程)期末作业 (5)
-1. 标题(TITLE)
“Quasi-Streaming Graph Partitioning: A Game Theoretical Approach”,这个标题可以被翻译成“准流式图划分:博弈论方法”。
- 准流式图划分(Quasi-Streaming Graph Partitioning):流式图划分是一种处理大规模图的算法。这种算法的特点是,它在任何时候只处理一部分的图数据,因此适合于处理大规模图数据。而”准流式”可能意味着这种算法在处理图数据时,做了一些优化或改进,以提高效率或减少内存使用。
- 博弈论方法(A Game Theoretical Approach):博弈论是一种用于理解决策制定者如何做出选择的数学理论。在这种情况下,博弈论可能被用来理解或设计图划分算法的决策过程。例如,每个节点在选择划分到哪个区域时,可能会根据博弈论的理论进行决策。
所以,这篇论文可能是关于一种新的图划分算法,该算法采用一种准流式的处理方式,并使用博弈论来优化决策过程。然而,具体的细节和结果还需要阅读实际的论文才能了解。
0. 摘要(ABSTRACT)
0.1. 理解(Comprehension)
这篇论文的摘要大致上解释了论文的主题和主要内容。以下是摘要的一些关键点的解释:
- 背景:图的划分是处理大规模图数据的基础问题。现有的图划分模型主要基于流式或离线方式。流式模型在进行决策时需要考虑所有先前边的划分选择,这使得并行划分困难。离线划分则需要完整的图输入,对于大规模的图可能不适用。
- 方法:作者提出了一种准流式划分模型,并使用博弈论为边划分问题提供了一个解决方案。作者将整个边流分为一系列批次,每个批次的大小是分割数的常数倍。在每个批次中,将图边的划分问题建模为一个博弈过程,其中边的划分选择被视为博弈中玩家的理性策略选择。因此,边划分问题被分解为在一系列博弈过程中寻找纳什均衡。
- 理论证明:作者数学证明了在这样的博弈过程中存在纳什均衡,并分析了收敛到纳什均衡所需的回合数。他们进一步通过计算混乱代价(Price of Anarchy, PoA)来衡量这些纳什均衡的质量,该值由分割数限定。
- 实验验证:作者通过在真实世界的图和随机图上的实验来评估策略的性能。结果显示,与现有的五种流式划分策略相比,作者的解决方案在负载均衡和复制因子方面取得了显著的改进。
复制因子(Replication Factor): 在图分割和分布式图处理的上下文中,复制因子通常指的是在多个分割或节点之间复制顶点或边的次数。这是一种处理图数据的策略,使得不同的分割或节点可以同时访问和处理某些图元素。 例如,假设你有一个大的图数据集,它被分割到多个服务器上进行处理。然而,一些图算法需要访问一个顶点的所有邻居。如果这些邻居分布在不同的服务器上,那么这个顶点可能需要在多个服务器上创建副本,以便每个服务器都可以访问到它的所有邻居。这个顶点在所有服务器上的副本总数就是其复制因子。 复制因子是一种权衡。一方面,高复制因子可以减少数据传输和通信开销,因为每个节点都有其需要的所有数据的本地副本。另一方面,高复制因子会增加存储和内存使用,因为每个顶点或边可能需要在多个地方存储。此外,如果图的结构发生改变,所有的副本都需要更新,这可能会导致一些同步问题。
纳什均衡是博弈论中的一个概念,指的是在一个博弈中,当所有玩家都对其他玩家的策略有了解,并且没有玩家能通过改变自己的策略来获得更好的结果的情况。
负载均衡是指在多个处理单元之间分配工作的方式,以使得每个处理单元处理的工作量大致相等,从而提高整体的处理速度和效率。
复制因子通常用于描述在分布式系统中数据复制的程度。在图的划分中,如果一个边的两个节点被划分到不同的部分,那么这个边可能需要被复制到这两个部分。复制因子越小,表示复制的边或顶点越少,系统的效率越高。
0.2. 翻译(Translation)
图分割是在大图上进行可扩展图计算的基本问题。现有的分割模型基于流处理或离线处理。在流处理模型中,当前的边需要所有先前边的分割选择来做出决定。因此,很难并行进行分割操作。此外,离线的分割需要对输入图的全面知识,这可能不适合大图。在这项工作中,我们提出了一个准流处理分割模型,并为边分割问题提出了基于博弈论的解决方案。具体来说,我们将整个边流分成一系列批次,其中批次大小是分割数的常数倍。在每个批次中,我们将图边分割问题建模为一个游戏过程,其中边的分割选择被视为游戏中的玩家的理性策略选择。因此,边分割问题被分解为在一系列游戏过程中找到纳什均衡。我们通过数学证明了这种游戏过程中纳什均衡的存在,并分析了收敛到纳什均衡所需的回合数。我们进一步通过计算PoA(无序代价)来衡量这些纳什均衡的质量,该值受到分割数量的限制。然后,我们通过在真实世界的图和随机图上的全面实验评估了我们的策略的性能。结果表明,与五种现有的流处理分割策略相比,我们的解决方案在负载平衡和复制因子方面实现了显著的改进。
1. 引言(INTRODUCTION)
1.1. 理解(Comprehension)
这篇论文的引言部分首先阐述了大规模图在许多实际应用中的应用,如网络图和在线社交网络。然后,它介绍了在分布式系统中进行图计算的挑战,特别是需要在机器之间划分整个图,以及图划分如何显著影响分布式图计算系统的通信成本和工作负载平衡。它还指出,现有的图划分策略可以分为顶点划分和边划分两种。
在顶点划分方案中,各个分割中的顶点是不相交的,边则跨越两个分割。在边划分方案中,边被划分到不同的分割,而顶点则跨越多个分割。此外,作者还指出,大多数真实世界的图都遵循幂律度分布,而边划分方案对于幂律图可以取得更好的性能。
然后,引言部分进一步讨论了一些现有的边划分策略的问题,如DBH和HDRF。例如,DBH总是选择度数高的顶点进行切割,这在实际的流式设置中可能行不通。HDRF使用部分度来帮助决策,但是这也可能不适用于真实的流式设置,因为在真实的流式设置中,无法提前计算全局度信息,而存储全局度表会消耗大量内存。
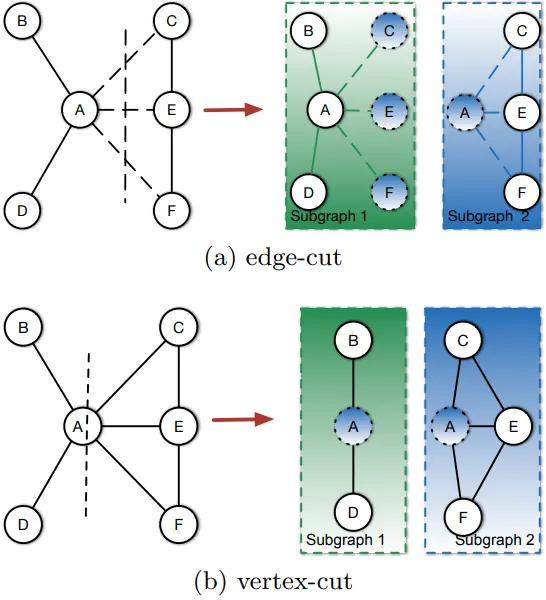
顶点分割和边分割的区别与联系
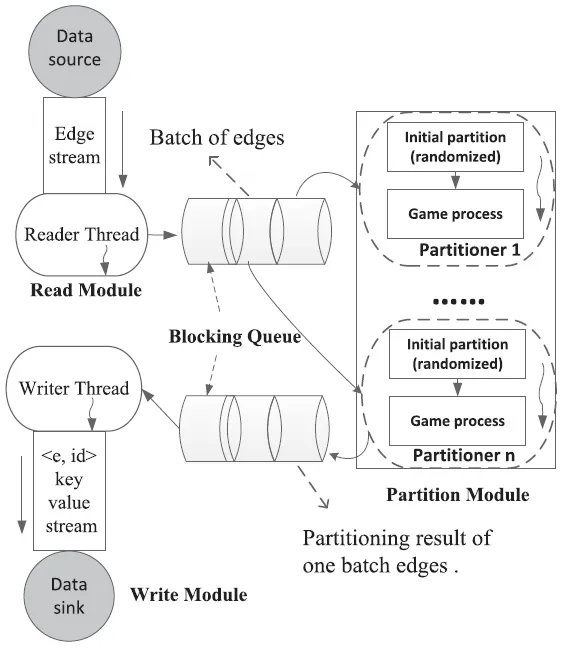
基于这些观察,作者提出了一种准流式模型和一个新的边划分策略。在这个模型中,整个边流被分成一系列的批次,每个批次的大小是输入参数。在每个批次中,所有的边构成了一个博弈过程的玩家集。每个边的划分选择被视为博弈中的理性策略。当每个批次的博弈过程达到纳什均衡,即没有边有动机单方面改变其当前的划分选择时,这个批次的划分任务就完成了。每个批次的划分任务可以由一个划分线程来完成,所有的划分线程可以并行进行。
作者指出,与流式模型和离线模型相比,他们的准流式模型的总内存消耗只是批次大小$\times$线程数,这比流式模型和离线模型的内存消耗都要小得多。此外,由于引入了并行性,准流式模型的时间消耗也可能减少。
最后,作者列出了他们的贡献,包括提出了解决边划分问题的准流式模型和基于博弈论的新型划分策略;他们数学证明了在准流式边划分博弈中纯纳什均衡的存在性,并分析了收敛到纳什均衡所需的回合数;他们证明了纳什均衡和社会最优之间的比例(即,无序性的代价,Price of Anarchy, PoA)在他们的边划分博弈中是由分割数量限制的;他们通过对大型真实世界图和随机图的综合实验评估了他们方法的性能。
准流式图分割模型
Price of Anarchy(PoA):
Price of Anarchy(PoA)是一个经济学和博弈论的概念,用于衡量在非合作博弈(也就是参与者做出的决策是为了最大化自身的利益,而不是整体的利益)中,个体理性行为可能导致的社会福利(总体效用)的损失。 具体来说,Price of Anarchy是指在一个非合作博弈中,达到纳什均衡(每个参与者都无法通过单方面改变策略来提高自己的收益)的总体效用与在全局最优(所有参与者都按照最优策略行动,以最大化总体效用)的总体效用之间的比例。 如果这个比例接近1,那么即使参与者按照自己的私人利益行动,总体效用也不会比全局最优的情况下低很多。然而,如果这个比例远小于1,那么个体的理性行为可能会导致总体效用大大降低。 在论文中,作者可能使用Price of Anarchy来衡量他们的算法在理想情况(全局最优)和实际情况(纳什均衡)之间的效用差距。这可以帮助读者理解算法的性能,并与其他算法进行比较。
在引言部分的最后,作者概述了论文的其余部分的结构,包括相关工作的介绍,系统模型和问题定义,具有理论分析的准流式边划分博弈的呈现,一个基于最佳响应动态的算法以找到纳什均衡,策略性能的评估,以及对工作的总结。
总的来说,这篇论文介绍了一种新的图划分策略,该策略基于博弈论,并利用准流式模型来解决大规模图划分问题。这种策略允许并行处理,以提高效率,并试图克服传统流式和离线图划分方法的局限性。
1.2. 翻译(Translation)
如今,大型图已经在各种真实应用中出现,如网页图和在线社交网络。从这些图中挖掘知识面临巨大挑战,因为它们的容量正在爆炸式增长。要在分布式系统上进行图计算,必须在多台机器间对整个图进行分割,这是一个必要的过程。图分割可以显著影响分布式图计算系统的性能,包括通信成本和工作负载平衡。现有的图分割策略可以分为两类:顶点分割和边分割。顶点分割导致不同分割中的顶点互不相交,边则跨越两个分割。相反,边分割导致边在不同分割中分离,顶点则跨越几个分割。顶点分割和边分割的区别在图1中有所说明。
在顶点分割方案中,每个分割的工作负载由其承载的顶点数量决定。通信成本由横跨不同分割的边的数量决定。在边分割方案中,每个分割的工作负载由其承载的边的数量决定。此外,通信成本由所有顶点的副本总数决定。顶点分割方案已被大多数分布式图计算框架采用,如Pregel[15],GraphLab[14]和Giraph[19]。
大多数真实世界的图遵循幂律度分布。已经证明,边分割方案可以为幂律图提供更好的性能[9]。因此,提出了几种基于边分割的策略,如DBH[24]和HDRF[18]。然而,DBH[24]利用全局度信息总是切割高度顶点。在真实的流处理环境中,这可能是不可行的,因为在流处理系统中,如[22],计算是连续且不间断的。至于HDRF[18],它使用部分度来帮助做出决定。它维护一个全局度表,每个顶点有部分度。当新的边到来时,两个端点的度都会更新。然而,这些解决方案在真实的流处理环境中也可能不适合。在真实的流处理环境中,无法提前计算全局度信息。此外,存储全局度表需要消耗内存,其中m是图的边的数量。对于一台商品机器来说,当图的边的数量超过一个限制时,这可能是无法接受的。
此外,在这样一个巨大的表中进行查找也可能效率低下。此外,基于流模型的现有解决方案缺乏并行性(更多细节请参见第3.1节)。例如,Stanton和Kliot[21]将并行执行流图分割视为他们的未来工作,如他们所说,“第二个方向是解决使用并行加载器…我们期望并行加载器在图流的独立部分上运行的性能…”。
基于这些观察,我们在本文中提出了一种准流模型和一种来自博弈论的新颖的边分割策略,如图2所示。在这个模型中,整个边流被划分为一系列批次,其中批次大小(一定数量的边)是一个输入参数。在每个批次中,所有的边构成了游戏过程中的玩家集合。边的分割选择被视为游戏中的理性策略。当每个批次的游戏过程达到纳什均衡,即没有边有动机单方面改变其当前的分割选择时,这个批次的分割任务就完成了。每个批次的分割任务可以由一个分割线程完成,该线程对应于图2中的分割器。所有的分割线程可以并行进行。如前所述,准流模型可能是从流模型中发现潜在并行性的一个有趣尝试[21],期望通过并行分割图流的独立部分获得类似的性能。
与流模型和离线模型相比,我们的准流模型的总内存消耗只有批次大小乘以线程数量,这比流模型和离线模型中的内存消耗都要小得多。此外,与流模型相比,由于引入了并行性,准流模型所用的时间也可能大大减少。这些理论分析在实验中也得到了证实(第6.2节)。
值得注意的是,大多数真实世界的图是通过广度优先的方式收集的[3],[25]。因此,当图被存储为边列表形式时,相同顶点的边被存储在彼此旁边。此外,大多数真实世界图的度遵循幂律分布,其中大多数顶点的度都很小。如果批次大小大于大多数顶点的度,我们可以将由每个批次组成的子图视为近似不相交的。因此,我们可以并行地对这些批次进行分割。我们需要指出,如果上述假设不成立,即如果一个顶点的边在输入中不连续出现,我们可以进行一个预处理步骤,更多的细节将在第6.2节给出。注意,准流模型的假设似乎比流模型的假设要强得多,因为在准流模型中,一个边可以根据同一批次中其他边的选择偏离其当前的分割选择(更多细节请参见第5节)。然而,在准流模型中,批次大小是分割数量的常数倍。因此,每个批次内的信息非常有限。相反,在流模型中,每条边可以通过一次通过的方式利用所有先前边的分割选择。因此,在准流模型中执行高效的分割可能比在流模型中更难。
2. 相关工作(RELATED WORK)
2.1. 理解(Comprehension)
在“相关工作”这一部分,作者提到了过去一些图划分策略的研究。图划分在并行和分布式图计算应用中起着关键作用,因为数据布局对于这些应用的性能有显著影响,包括通信成本和工作负载平衡。由于图划分的固有难度,许多启发式划分策略已经被提出。
现有的启发式划分策略大致可以分为离线基础和流式基础两类。METIS是一种广受好评的离线启发式,它结合了许多启发式,比如著名的Kergnighan-Lin启发式。然而,离线基础的启发式需要关于图的全部信息,这对于大规模图和动态图可能是不切实际的。在Powerlyra中提出了一种混合启发式,该启发式将顶点划分和边划分方案结合在一起。这种混合启发式被称为Ginger,在原始划分之后,需要对高度顶点进行额外的重新分配阶段。
在流式设置中首次引入了平衡图划分问题的是Stanton。他提出了几种贪婪策略,这些策略根据负载平衡和每个分割中承载的邻居数量来分配当前顶点。Fennel是另一种顶点划分方案,它结合了两种启发式:将新到达的顶点放在承载最多邻居或承载最少非邻居的分割中。请注意,作者在另一项研究中实现了Fennel的边划分版本。
对于特定的顶点划分问题,提出了一种基于博弈论的解决方案,这与传统的流式图顶点划分在设置和优化目标上都有很大的不同。流式边划分的启发式首次在另一项研究中被提出,其中证明了边划分方案对于幂律图比顶点划分方案更有效。另外两种流式边划分方案,DBH和HDRF利用了自然图的偏度分布特性。关于图划分启发式的调查可以在另一项研究中找到。
这一部分提供了图划分领域的一个背景,让读者了解到过去的研究以及他们的局限性,从而强调了他们提出的新方法的重要性和贡献。
2.2. 翻译(Translation)
图分割在并行和分布式图计算应用中起着关键作用,因为数据布局对这些应用在通信成本和工作负载平衡方面的性能有着显著影响。由于图分割的内在难度[1],[8],实践中提出了许多启发式分割策略。最先进的启发式分割策略可以分为离线和流式两种。METIS[20]是一种广受好评的离线启发式方法,它结合了大量的启发式方法,如众所周知的Kergnighan-Lin[12]启发式方法。然而,离线的启发式方法[11]需要对图的全部知识,这对大规模图和动态图可能是不切实际的。Powerlyra[7]提出了一种混合启发式方法,将顶点分割和边分割方案结合在一起。这种混合启发式方法被称为Ginger,在原始分割后,高度顶点需要进行额外的重新分配阶段。
在流设置中首次引入了平衡图分割问题的是Stanton[21]。在他的工作[21]中提出了几种贪婪策略,根据负载平衡和每个分割中承载的邻居数量来将当前顶点分配到分割。Fennel[23]是另一种顶点分割方案,它结合了两种启发式方法:将新到达的顶点放在持有最多邻居或持有最少非邻居的分割中。请注意,作者在他们的工作[5]中实现了Fennel的边分割版本。在他们的工作[2]中提出了一种基于博弈论的特定顶点分割问题的解决方案,这在设置和优化目标方面与传统的流图顶点分割[21]完全不同。
首次提出流式边分割的启发式方法是在工作[9]中,其中已经证明,对于幂律图,基于边分割的方案比基于顶点分割的方案更有效[9]。另外两种流式边分割方案,DBH[24]和HDRF[18],利用了自然图的偏度分布特性。关于图分割启发式的调查可以在工作[6]中找到。
3. 系统模型和问题定义(SYSTEM MODEL AND PROBLEM DEFINITION)
3.1. 系统模型(System Model)
在“系统模型与问题定义”这一节的“系统模型”小节中,作者首先介绍了已经被深入研究的流式划分模型。在流式顶点划分问题中,顶点与其邻居集合一起到达;在流式边划分问题中,每条边与其两个端点一起到达。在这两种变体中,启发式决定将当前顶点或边放置在某个分割上,这个决定是基于所有先前顶点或边的划分选择,这是通过维护一个全局表来实现的,该表记录了所有先前顶点或边的划分选择。
然后,作者提到了一些存在的问题,例如基于度的启发式(如DBH和HDRF)在边划分问题中,需要维护一个额外的度表来记录每个顶点的度信息。在实际的流式场景中,流可能非常大甚至无限大,因此这些解决方案在巨大表的内存使用和在这样一个巨大表上的低效查找方面可能是低效的。此外,由于全局表的读取和写入强度大,很难并行进行划分。
为了解决这些问题,作者提出了准流式模型,目标是实现更多的并行性和更少的内存使用。他们定义了准流式划分模型,全图由一个边流表示,每条边与其端点一起到达。整个流被划分为一系列批次,批次大小作为一个输入参数,它是分割数量的常数倍。分割数量k也是一个输入参数。在每个批次中,划分问题被建模为一个博弈过程。当找到一个纳什均衡时,这个批次的划分就完成了。
在准流式模型中,当前边可以通过迭代的方式充分利用同一批次内其他边的划分选择,这可以比基于流式的解决方案实现更好的局部最优。无需维护一个巨大的全局表来记录所有先前边的选择,我们只使用一个本地表来记录同一批次内其他边的选择,这比全局表小得多。此外,当当前批次完成其划分后,可以重用本地表的内存。
在后续的章节中,作者将给出更多的细节,包括找到纳什均衡的方法,以及如何基于最佳响应动态的算法。
3.2. 策略博弈理论(Strategic Game Theory)
作者将边分割问题在每一批次(batch)中建模为一种博弈的方法。在博弈论中,博弈的每个参与者(在这篇论文中,参与者是边)被假设为自私且理性的,每个参与者都试图优化自己的目标函数(或者说最小化自己的成本函数)。
作者在这里进一步解释,每个参与者(即每条边)在选择一种策略(即选择被分到哪个分割)来最小化自己的成本时,并不考虑自己的选择对其他参与者的目标函数的影响。这是博弈论中所说的”自私”和”理性”的含义:每个参与者都关心的是自己的利益,而不是整个系统的利益。
“Formally, a strategic game is defined as:…”这句话似乎是在为接下来的定义做铺垫,可能会提到博弈的参与者、策略空间和目标(或成本)函数等元素。然而,由于这句话后面的内容并没有给出,所以无法给出更具体的解释。
- 玩家列表 $\mathbb{N}=\{1,2,\dots,N\}$;
- 策略空间 $\mathbb{S}=S_1\times S_2\times\cdots\times S_N$,其中$S_i$是第$i$个玩家的策略;
- 策略实例 $S=(S_1,S_2,\dots,S_N) \in\mathbb{S}$ ,也有$S=(S_i,S_{-i})$;
- 代价函数 $C_i(S): \mathbb{S}\rightarrow\mathbb{R}$,策略实例对于第$i$个玩家的策略的代价;
- 策略博弈 $\mathbb{G}=\{\mathbb{N},\mathbb{S},\{C_1,C_2,\dots,C_N\}\}$ 唯一表示;
- 社会福利 $\sum_{i\in\mathbb{N}}C_i(S)$,目标是最小化所有玩家的总代价。
定义1、2:
- A pure strategy provides a complete definition of how a player will play a game for any situation.
- The pure strategy profile $S^*\in\mathbb{S}$ is pure strategy Nash Equilibrium iff for each $i\in\mathbb{N}$:
\begin{equation} C_i(S^*_i,S^*_{-i})\leq C_i(S’_i,S^*_{-i}) \end{equation}
where $S’\neq S^*,S’\in S_i$ is another strategy。
3.3. 问题定义(Problem Definition)
定义:整个图流(Graph Stream)⁍中的每批(Batch)表示为子图⁍
$$ \begin{equation} \min{1\over|V|}\sum_{v\in V}|Rep(v)|,\space\text{s.t.}\max_{p_i\in P}L(p_i)<\lambda{|E|\over k} \end{equation} $$
其中$Rep(v)\subseteq P$为顶点$v$的所有副本(replicas including master replica and mirror replicas) $\lambda\geq1$是一个很小的常数,$P=\{p_1,p_2,…,p_k\}$是分割集合,$L(p_i)$表示$p_i$所有批的边数和;也就是说,$\sum_{i=1}^kL(p_i)=|E|$。边分割时一个NP-hard问题。
本文中的图分割质量是通过以下两个指标来衡量的:
- $\sigma$(Standard deviation of edge load):每个分割中承载的边数的标准差;
- $rep$(Replication factor):每个顶点的平均复制次数,定义为${1\over|V|}\sum_{v\in V}|Rep(v)|$。
我们的负载均衡指标$\sigma$不同于相对标准偏差(Relative Standard deviation)指标,后者被定义为$\sigma$与平均负载的比率。$\sigma$度量也不同于最大负载与平均负载之比的度量。请注意,我们的偏差标准$\sigma$是比这两个衡量负载平衡状态的指标更严格的指标,这可能会在负载平衡方面进一步区分分割策略。
4. 准流式边分割博弈模型(QUASI-STREAMING EDGE PARTITION GAME)
4.1. 博弈构建(Game Construction)
作者试图将边划分问题建模为一个博弈过程。在这个过程中,每一条边被视为一个玩家,边的划分选择相当于玩家的策略选择。在博弈过程中,当找到纳什均衡时,表明我们已经找到了社会福利目标的局部最优解。因此,作者希望通过在边划分问题的目标函数和博弈过程中的社会福利函数之间建立一个桥梁,探讨是否可以找到边划分问题的一个良好的局部最优解。
在这一节中,作者首先构建了一个与边划分问题相关的博弈过程。然后他们证明了这个博弈过程总是可以收敛到一个纳什均衡。最后,他们通过PoA(Price of Anarchy,即无政府状态的代价)来衡量这些纳什均衡的质量。这篇论文中使用的主要符号及其描述在论文的表1中列出。
简单来说,作者在这一节中提出了一个新颖的方法,将图的边划分问题建模为一个博弈过程,然后通过这个博弈过程寻找到问题的局部最优解。这个方法的优点是可以在实时处理大规模图数据的同时,保证了解的质量,因为找到纳什均衡就意味着找到了问题的局部最优解。
首先,我们定义每个batch中的边分割目标函数QGEP(Quasi-streaming Graph Edge Partitioning)如下:
$$ \begin{equation} QGEP(G_b,P)=\alpha\beta\sigma^2+(1-\alpha)\sum_{v\in V_b}|Rep(v)|\end{equation} $$
其中$G_b$表示为batch $b$代表的子图,$P$是一个分割。$\sigma$是“问题讨论”提到的每个分割中边负载的标准偏差。$\alpha\in(0,1)$是这两个指标之间的偏好因子。$\beta$是归一化因子,将在后面正则化问题中详细讨论。根据$QGEP$目标函数,我们定义边划分博弈的社会福利函数如下:
$$ \begin{equation} C(S)=\alpha\beta{1\over k}\sum_{i=1}^kl^2(p_i)+(1-\alpha)\sum_{v\in V_b}|Rep(v)|\end{equation} $$
其中$S=(S_1,S_2,\dots,S_N) \in\mathbb{S}$是一个策略实例,$l(p_i)$是子图$G_b=(V_b,E_b)$在分割$p_i$中的边数之和;并且有$\sum_{i=1}^kl(p_i)=|E_b|$。接下来我们来证明$C(S)$和$QGEP$的等价性。
命题1. 社会福利$C(S)$与$QGEP$的目标函数之差是一个常数值。
证明1. 因为
$$ \begin{equation}\begin{split} \sigma^2&={1\over k}\sum_{i=1}^k(l(p_i)-a)^2 \\ &={1\over k}\Bigg[\sum_{i=1}^kl^2(p_i)-2a\sum_{i=1}^kl(p_i)+ka^2\Bigg] \\&={1\over k}\Bigg[\sum_{i=1}^kl^2(p_i)\Bigg]-{2a|E_b|\over k}+a^2 \\&=\sum_{i=1}^kl^2(p_i)-a^2 \end{split} \end{equation} $$
所以$QGEP=\alpha\beta\sigma^2+(1-\alpha)\sum_{v\in V_b}|Rep(v)|=C(S)-\alpha\beta a^2$
我们对单条边$e$的分配到分割$S_e\in P$的个体代价定义为$C_e(S)$,计算方法如下:
$$ \begin{equation} C_e(S)=\alpha\beta{1\over k}l(S_e)+(1-\alpha)\Bigg({1\over d(S_e,u)}+{1\over d(S_e,v)}\Bigg) \end{equation} $$
$e$两端的顶点是$u$和$v$,并且$d(S_e,u)$和$d(S_e,v)$分别是以$u$和$v$为顶点的边的数量。
命题2. 社会福利$C(S)$是该博弈中所有边的个体成本之和,也就是
$$ \begin{equation}\begin{split}\sum_{e\in E_b}C_e(S)&=\sum_{e\in E_b}\Bigg[{\alpha\beta\over k}l(S_e)+(1-\alpha)\sum_{e\in E_b}\Bigg({1\over d(S_e,u)}+{1\over d(S_e,v)}\Bigg)\Bigg]\\&={\alpha\beta\over k}\sum_{i=1}^k\sum_{e\in E(p_i)}l(p_i)+(1-\alpha)\sum_{i=1}^k\sum_{S_e\in p_i}\Bigg[{1\over d(S_e,u)}+{1\over d(S_e,v)}\Bigg]\\&={\alpha\beta\over k}\sum_{i=1}^kl^2(p_i)+(1-\alpha)\sum_{i=1}^k\sum_{w\in V_b\\,\space p_i\in Rep(w)}{|incident(p_i,w)|\over d(p_i, w)}\\&={\alpha\beta\over k}\sum_{i=1}^kl^2(p_i)+(1-\alpha)\sum_{i=1}^k\sum_{w\in V_b}1\{p_i\in Rep(w)\}\\&={\alpha\beta\over k}\sum_{i=1}^kl^2(p_i)+(1-\alpha)\sum_{w\in V_b}| Rep(w)|\\&=C(S)\end{split}\end{equation} $$
因此将构建的博弈表示为EPG(Edge Partition Game),$EPG=\{E_b,\mathbb{S},\{C_e|e\in E_b\}\}$
4.2. 正则化问题(Normalization Issue)
需要注意的是如果没有正则化参数$\beta$,社会福利函数中负载均衡部分$C^{BAL}=\alpha{1\over k}\sum_{i=1}^kl^2(p)$和复制因子部分$C^{REP}(S)=(1-\alpha)\sum_{v\in V_b}|Rep(v)|$在数值上是不可比较的;如果没有规则化,负载均衡部分可能会远大于复制因子部分。因此我们需要引入正则化参数$\beta$使得两部分在数值上可比较。当偏好值$\alpha=0.5$时,负载均衡部分应该和复制因子部分在数值上相等,也就是
$$ \begin{equation}\beta{1\over k}\sum_{i=1}^kl^2(p_i)=\sum_{v\in V_b}|Rep(v)|\Rightarrow\beta={k\sum_{v\in V_b}|Rep(v)|\over\sum_{i=1}^kl^2(p_i)} \end{equation} $$
接着我们给出$\beta$的有效范围。
命题3:$\sum_{i=1}^kl^2(p_i)$最大值为$|E_b|^2$,发生在所有的边都分配到1个分割的时候;最小值为$|E_b|^2\over k$,发生在所有的边平均分配到每一个分割。(此命题在Appendix A中证明)
命题4:$\sum_{v\in V_b}|Rep(v)|$的最小值为$|V_b|$,发生在当所有的顶点都只有1个副本;最大值为$k|V_b|$,发生在所有的顶点都有k个副本。
命题5:基于命题3和命题4,$\beta$的范围${k|V_b|\over|E_b|^2}\leq\beta\leq {k^3|V_b|\over|E_b|^2}$
4.3. 精确势能博弈(Exact Potential Game)
可以证明上述的边分配博弈是一个精确势能博弈(Exact Potential Game),也就是说,这个博弈模型一定存在一个纯策略的纳什均衡。
定义3:博弈$\mathbb{G}=\{\mathbb{N},\mathbb{S},\{C_1,C_2,\dots,C_N\}\}$是一个精确势能博弈当且仅当存在一个函数$\Phi:\mathbb{S}\longmapsto\mathbb{R}$,使得$\forall i\in \mathbb{N}$,都有
$$ \begin{equation}\Phi(S_i’,S_{-i})-\Phi(S_i,S_{-i})=C(S_i’,S_{-i})-C(S_i,S_{-i}) \end{equation} $$
其中$S_i’\neq S_i,S_i’\in S$是另一个策略。
定理1:博弈 $\mathbb{G}=\{\mathbb{N},\mathbb{S},\{C_1,C_2,\dots,C_N\}\}$是一个精确势能博弈。(Appendix B中证明)
4.4. 无序代价(Price of Anarchy)
PoA是所有纳什均衡策略中最糟糕的社会福利和所有策略中最优的社会福利的比值。它是衡量纳什均衡质量的重要指标。为了社会福利成本最小化目标,PoA正式定义为:
$$ \begin{equation}PoA={\max_{S\in PNE}C(S)\over OPT} \end{equation} $$
$PNE\subseteq\mathbb{S}$是所有纯策略纳什均衡构成的集合。OPT是成本最小化问题社会福利全局最小值。
命题6:记$OPT_{\min}^{BAL}$,$OPT_{\min}^{REP}$和$OPT_{\min}$分别是$C^{BAL}(S)$、$C^{REP}(S)$和$C(S)$最小值,其中$C^{BAL}(S)=\alpha\beta{1\over k}\sum_{i=1}^kl^2(p)$,$C^{REP}(S)=(1-\alpha)\sum_{v\in V_b}|Rep(v)|$,因此我们有
$$ \begin{equation}OPT_{\min}^{BAL}+OPT_{\min}^{REP}\leq OPT_{\min}\end{equation} $$
类似的,我们很容易得到$OPT_{\max}^{BAL}+OPT_{\max}^{REP}\geq OPT_{\max}$,其中$OPT_{\max}^{BAL}$,$OPT_{\max}^{REP}$和$OPT_{\max}$分别是$C^{BAL}(S)$、$C^{REP}(S)$和$C(S)$最大值。
证明6:记$S^{*BAL}$、$S^{REP}$和$S^{}$分别表示取得$C^{BAL}(S)$、$C^{REP}(S)$和$C(S)$最小值的策略,因此我们有
\begin{equation} \left\{\begin{array}{lr} C^ {BAL}(S^*)\geq C^{BAL}(S^{*BAL})\\ C^{REP}(S^*)\geq C^{REP}(S^{*REP}) \end{array} \right.\end{equation}
$$ \begin{equation}\begin{split} & C(S^*)=C^{BAL}(S^ *)+C^{REP}(S^ *)\geq C^{BAL}(S^ {*BAL})+C^{REP}(S^{*REP})\\ & \Rightarrow OPT_{\min}\geq OPT_{\min}^{BAL} + OPT_{\min}^{REP} \end{split} \end{equation} $$
命题7:博弈$\mathbb{G}=\{\mathbb{N},\mathbb{S},\{C_1,C_2,\dots,C_N\}\}$的PoA的边界是$k$。(Appendix C中证明)
5. 最佳响应动态和回合复杂性(BEST RESPONSE DYNAMICS AND ROUND COMPLEXITY)
5.1. 最佳相应动态算法(Best Response Dynamics Algorithm)
详细介绍如何基于“最佳反应动态”理论找到一个纯粹的纳什均衡,及该过程的收敛速度如何。
“最佳反应动态”是一个在博弈论中常见的理论,它的基本思想是,每个玩家在给定其他玩家策略的情况下,选择自己的最佳反应。在这里,作者将此理论应用于边划分博弈中,即,每条边(作为玩家)在给定其他边的划分选择的情况下,选择自己的最佳划分;表示为算法1所示。

具体来说,他们在算法2中提出了一种基于算法1的变种。在算法2中,作者使用随机策略的划分结果作为博弈过程的起点,即,每条边以相等的概率随机选择一个划分。对于每条边,他们计算最小成本并记录相应的划分ID。如果最小成本的划分不是当前的选择,那么边会改变其选择以获得最小成本。迭代子程序将继续进行,直到在某一轮次中没有边更改其划分选择为止。
此时可以达到纯策略纳什均衡,表示每条边该分配到哪个分割。

作者通过在算法2的一个实例中计算结果,详细展示了这个过程。在这个例子中,每条边首先随机选择一个初始划分,然后在每一轮中,每条边都会基于个体成本函数计算其最佳反应,即它可以获得最小成本的地方。例如,在第一轮中,边$e_1$的最佳反应是$p_1$。如果没有边在第二轮中改变当前的划分选择,那么就找到了纳什均衡,也就是说,这个批次的划分任务完成了。
简单来说,这一小节介绍了如何使用“最佳反应动态”算法找到边划分问题的纳什均衡,也就是局部最优解。这种方法的优点是能够快速收敛,并且在实践中表现出较高的效率。

表2展示了算法2在图3上的计算过程。首先,每条边随机选择一个初始分割,例如,边$e_1$选择分割$p_1$。然后,在每一轮中,每条边都根据其个体成本函数(公式(6))计算其最佳响应,该函数可以获取最小成本。最佳响应以下划线标记。例如,边$e_1$在第1轮的最佳响应是p1。每行中的灰色填充单元格对表示一条边(以粗体字标记)的策略转变。例如,边$e_2$在第1轮中将其分割从$p_1$改变为$p_2$。注意,在第2轮中,没有边改变其当前分割选择,所以在第2轮找到了纳什均衡,也就是说,这一批次的分割任务已经完成。
5.2. 回合复杂度(Round Complexity)
现在分析算法2的回合复杂性,也就是算法收敛到纯策略的纳什均衡所需要的回合数和图规模之间的关系。调和序列$H(n)=\sum_{i=1}^n{1\over i}$,然后定义势能函数$\Phi(S)$如下:
$$ \begin{equation}\Phi(S)={1\over k}\alpha\beta\sum_{i=1}^k\sum_{j=1}^{l(p_i)}j+(1-\alpha)\sum_{v\in V_b}\sum_{i=1}^kH(d(p_i,v)) \end{equation} $$
为了计算出回合复杂度,我们调整势能函数使得其只取整数$\Phi_{\mathbb{Z}}(S)=c\Phi(S)$,有如下命题。
命题8:博弈$\mathbb{G}=\{\mathbb{N},\mathbb{S},\{C_1,C_2,\dots,C_N\}\}$的回合复杂度为$O(c|V_b|\ln|V_b|+c|V_b|)$。
6. 实验(EXPERIMENTS)
在本节中,我们评估我们的分割策略的性能。第6.1节描述了实验设置,包括系统模型、环境描述和使用的数据集。第6.2节描述了如何预处理输入以防它不满足一个顶点的边不连续出现的假设。第6.3节分别展示了基于流式、准流式和离线模型的最先进的分割方法的时间和内存消耗。第6.4节与其他五种最先进的流式边分割结果进行比较。
解释如下:
- 第6.1节是关于实验的设置:这里他们将会介绍用于实验的系统模型(也就是他们运行实验的硬件和软件环境),环境描述(可能包括运行实验的具体条件和参数设置),以及他们使用的数据集(实验的输入数据)。
- 第6.2节是关于数据预处理:在这部分,他们将说明如何对数据进行预处理,以确保它符合某些特定的假设,例如,一个顶点的相邻边不连续出现。
- 第6.3节是关于实验结果:他们将展示基于流式、准流式和离线模型的最先进的图分割方法的运行时间和内存消耗。
- 第6.4节是关于与其他方法的比较:他们将把他们的方法得到的图分割结果与其他五种最先进的流式边缘分割方法进行比较。
6.1. 实验设置(Experiment Setup)
我们实现了一个独立版本的图分割器,可以在图加载阶段捕捉分布式图计算系统的行为。所有实验(除了第6.2节中的模型比较)都基于图2所示的准流模型,这意味着所有竞争策略都以批处理方式对整个图进行分割。换句话说,每个批次是分割的基本单位。当所有批次完成他们的分割任务后,整个图的分割任务就完成了。例如,在准流模型下,采用贪婪策略的边只能利用同一批次内边的分割选择。DBH[24]只使用每个批次内的度信息。其他策略以类似的方式进行分分割。图2中的数据源和数据接收器对应于我们实现中的硬盘。
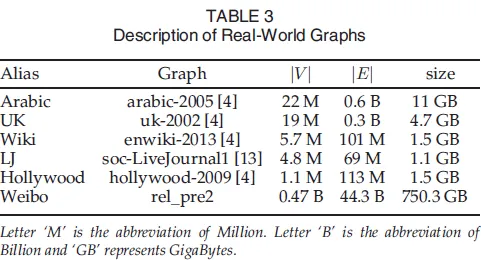
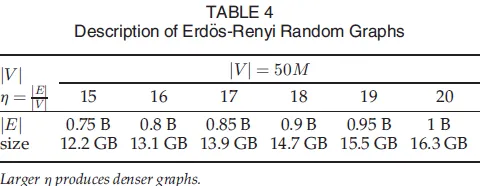
所有实验都在一台单机上进行,该机器配备有两个十五核的Gold 6151 CPU,扩展到60个虚拟CPU,960GB内存,运行CentOs Linux Release 7.3(内核3.10.0-514.el7)和JDK1.8.0。JVM的最大堆大小设置为950GB。我们使用的真实世界图数据集[4],[13]和随机图数据集分别列在表3和表4中。随机图数据集是基于Erdos-Renyi随机图模型通过SNAP[13]生成的。对于所有六种分割策略,为了消除流顺序的影响,我们在处理之前对每个批次进行洗牌。
为了方便,我们将我们基于博弈论的策略称为Mint。如果没有明确声明,我们的准流模型的默认参数设置如下。批次大小B设置为6400,分割线程的数量设置为60,这适用于所有竞争策略。此外我们设置$\alpha=0.5$,$\beta={k^3|V_b|\over 2|E_b|^2}$,其中$k$是分割的数量,$|E_b|$和$|V_b|$为每批子图的边和顶点的数量。
我们通过第3.3节中提到的指标评估我们方法的性能。
6.2. 预处理(Preprocessing)
正如引言中所提到的,我们的算法是基于这样的假设,即同一顶点上的边在输入中连续出现。因此如果输入的图不满足这个假设,我们需要进行一个预处理步骤。
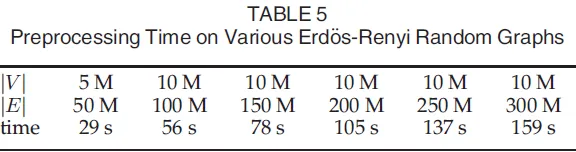
我们使用的预处理方案是一个支持多线程的哈希表。边的一个顶点用作哈希表的索引键,另一个顶点被添加到对应于索引键的列表中(类似于邻接表)。因此,预处理步骤的时间复杂度是$O(|E|)$,其中$|E|$表示图中的边的总数。
我们设计了一个实验来评估预处理的实际时间消耗。首先,我们生成一个Erdos-Renyi图[13],顶点的边存储在彼此相邻的位置;其次,我们对图中的所有边进行随机化;第三,执行预处理步骤。我们使用的Erdos-Renyi图和预处理所花费的时间已经列在表5中。从这个表中,我们可以看到,多线程预处理器的执行时间与图中边的数量线性相关。在以下的性能评估中,我们假设所有的图要么已经被预处理,要么满足同一顶点上的边连续出现的假设。
6.3. 与流式和离线模型的性能比较(Performance Comparisons with Streaming and Offline Models)
在这一部分,我们将首先比较我们的准流式模型与流式和离线模型在时间和内存消耗方面的表现。然后,我们将比较准流式和流式模型在复制因子和边负载标准差方面的分割质量。准流式模型的算法是Mint,我们选择了流式模型的最新算法HDRF[18]和离线
模型的METIS[11]进行比较。如第6.1节所述,我们使用Mint的默认设置。对于HDRF [18],我们设置的参数与作者的设置相同。对于METIS,我们使用手册上声明的默认分割策略。时间和内存比较分别在图5和图6中描绘。
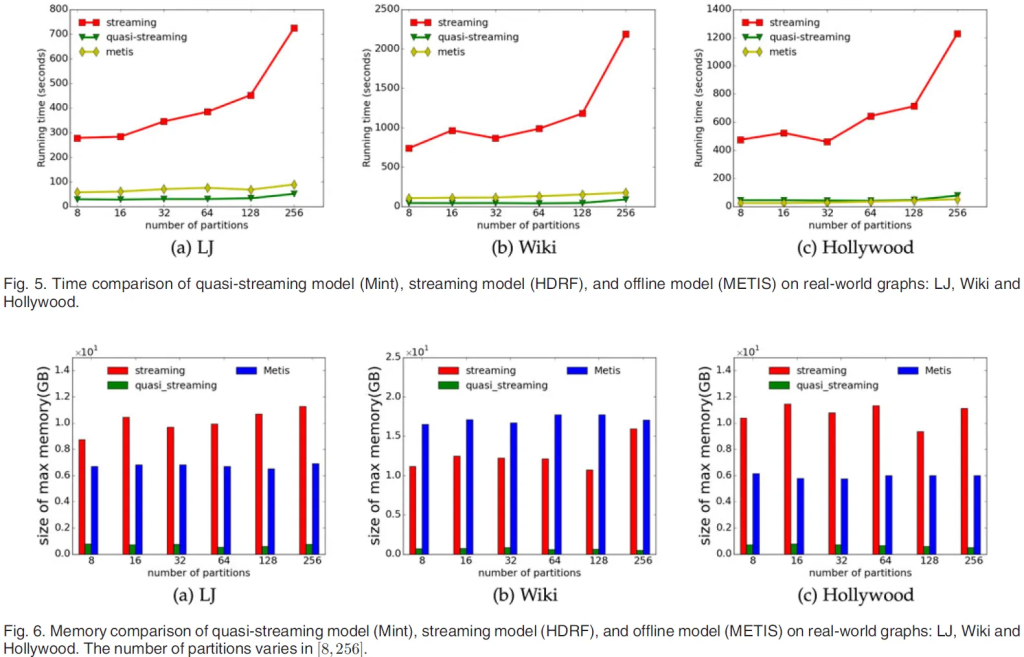
如图5所示,流式模型所花费的时间比准流式和离线模型都长得多,且随着分割数量的增加,这个差距甚至还在增加。另外,准流式模型所消耗的时间与离线模型相当。
至于内存消耗,图6显示流式和离线模型占用的内存比准流式模型多得多,这证实了第1节中提到的理论分析。
请注意,尽管准流式模型在时间和内存消耗上都优于流式模型,但分割质量相对较差,这可以在表6和7中找到。原因是,与每条边只能在由固定数量边组成的相应批次内决定其分割选择的准流式模型相比,在流式模型中,每条边都可以利用所有先前边的分割选择。因此,流式模型可以实现近乎最优的边负载平衡和较小的复制因子。
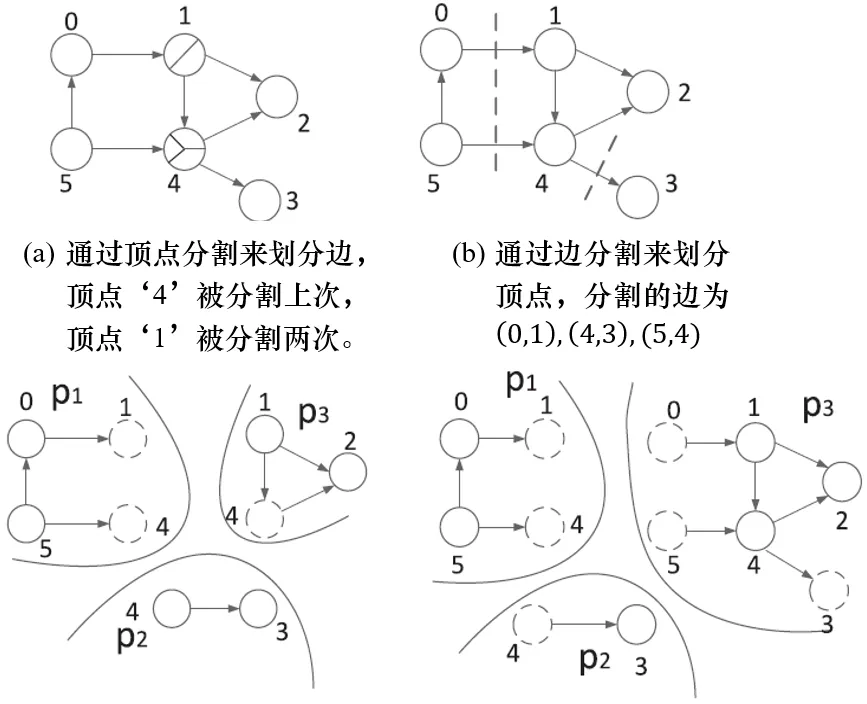
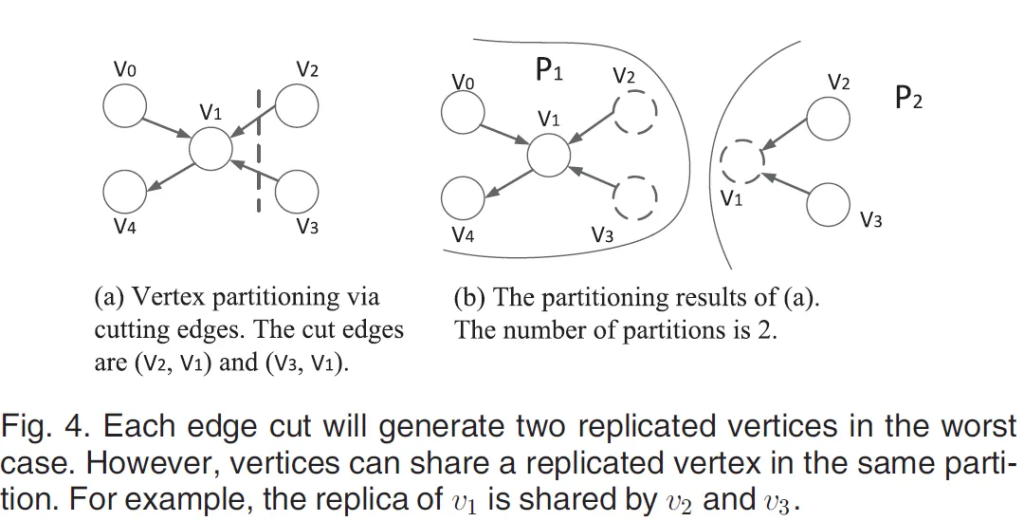
我们并没有比较准流式模型中的Mint算法和离线模型中的METIS算法之间的两个分割指标。原因一方面是,准流式模型接近流式设置,远离离线模型,因为批次大小是分割数量k的常数倍。另一方面,METIS是一个基于顶点分割的策略,其中分割质量是通过边割来衡量的。一个直接的观察是,每个边割在最坏的情况下将生成两个复制顶点[18]。因此,METIS的复制因子可以大致估计为$2\times|E_{cut}|\over|V|$,其中$E_{cut}$是METIS的割边集。然而,这对METIS可能相当不公平,如图4所示。如果我们只是断言每个边割将产生两个复制顶点,我们将在图4中得到4个复制顶点。但实际的复制顶点的数量是3,因为顶点$v_2$和顶点$v_3$可以在分割$p_2$中共享$v_1$的同一复制顶点。因此,我们没有与METIS比较分割指标。
6.4. 与准流模型中的其他策略的分割质量比较(Partitioning Quality Comparisons with Other Strategies within the Quasi-Streaming Model)
在本节中,我们将通过负载平衡指标$\sigma$和复制因子指标$Rep$(在第3.3节中定义)来比较我们的解决方案与其他五种最新的流式划分策略的性能。这五种其他的流式划分策略是Greedy[21]、Fennel[23]、DBH[24]、HDRF[18]和Random策略,其中每个边都以等概率从分割集中随机选择一个分割。注意,第一个贪婪策略用于顶点划分,首次在[21]中提出。Fennel是另一种顶点划分策略。我们参考了[5]、[18]中提供的边划分版本。可以在VGP$^2$和BGEP$^3$中找到贪婪和Fennel的分割分版本的实现细节。
我们使用随机策略来获得Mint的初始划分。对于HDRF[18],我们将设置参数$\lambda=3$,$\epsilon=1$使得其与作者的设置相同。考虑到[18]中的贪婪边划分版本可能会导致严重的负载不平衡,我们通过将平衡因子$\lambda$从1调整到3来微调原始实现,以便在划分过程中更多地关注负载平衡部分。DBH是散列策略的一种变体,它利用了真实世界图表中的倾斜度分布。随机策略类似于哈希策略,每个边都以相等的概率从分割集中选择一个分割。系统模型和Mint的参数遵循第6.1节中给出的实验设置中的默认设置。
真实世界图表(除微博外)和随机图表的复制因子比较如图7所示。如图7所示,Mint在所有六种划分策略中始终可以实现最小的复制因子。为了量化改进,我们定义了复制因子改进比率如下:
$$ \begin{equation} \gamma_{strategy}^{Rep}={Rep_{strategy}-Rep_{Mint}\over Rep_{strategy}}\times100\% \end{equation} $$
其中$Rep_{strategy}$表示特定策略的复制因子,$\gamma^{Rep}_{strategy}$表示Mint在复制因子方面对特定策略的定量改进。然后,列出了所有数据集的最大和平均复制因子改进比率结果,其中分割数量在[8,256]变化。如表8所示,与HDRF和随机策略比较,Mint可以在复制因子改进比率方面实现最高39.8%和78.2%的降低。注意,复制因子是一个很难最小化的指标:当复制因子减少一时,复制顶点的总数将减少$|V|$。
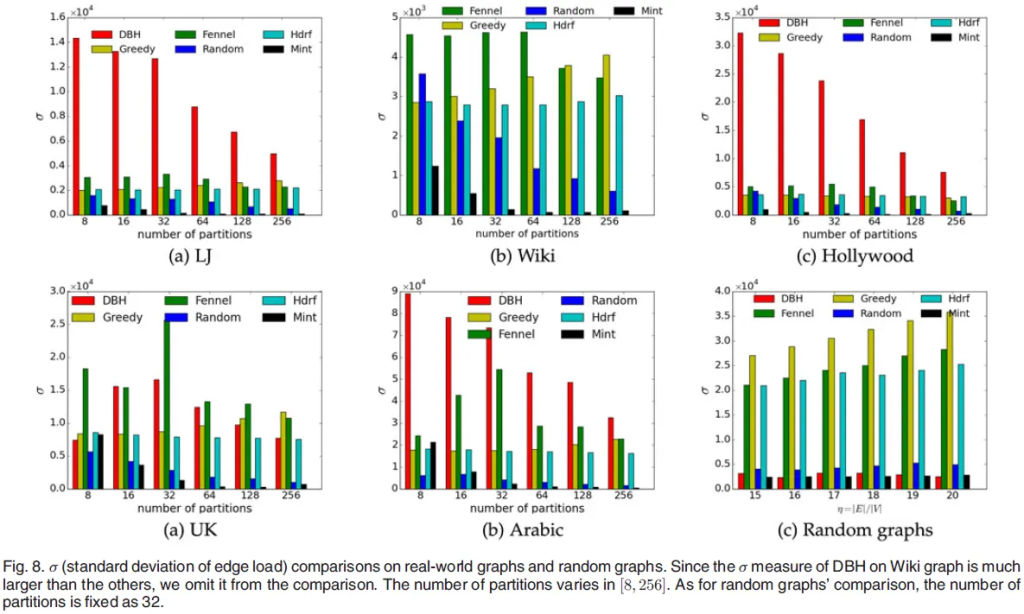
真实世界图表(除微博外)和随机图表的$\sigma$指标比较如图8所示。DBH在Wiki图表上的sigma指标远大于其他五种策略,因此我们在图8b中省略了它。如图8所示,与其他五种策略相比,Mint实现了远小的$\sigma$指标。同样,为了定量衡量改进,我们定义了$\sigma$指标改进比率如下:
$$ \begin{equation}\gamma_{strategy}^{\sigma}={\sigma_{strategy}\over\sigma_{Mint}} \end{equation} $$
其中$\sigma_{strategy}$表示特定策略的负载平衡指标,$\gamma_{strategy}^{\sigma}$表示Mint在负载平衡指标方面对特定策略的定量改进。最大和平均$\sigma$指标改进比率结果列在表9中,其中分割数量在[8,256]间变化。如表9所示,有一种情况,即当在Wiki图表上使用64个分割比较两种策略时,Mint可以实现比DBH小830倍的$\sigma$指标。在这种情况下,DBH和Mint的$\sigma$指标分别为50963.3199和61.3541。$\sigma$指标的显著降低实验证明了社会福利函数和QGEP的目标函数之间的紧密关联,这在命题1中得到了证明。
现在我们将展示在准流式模型下对微博图表的划分性能。这个图表包含了0.47亿个顶点和44.3亿个边,其图表大小约为Wiki图表的500倍。根据表10,我们可以看到,我们的Mint算法的复制因子和边负载的标准偏差都比其他五种策略要好。这与Mint算法在之前显示的小尺寸图表上的划分结果相一致。另外,使用不同策略处理微博图表的平均时间大约需要21千秒。这也符合在较小尺寸图表上的处理效率(处理时间与边数的比值)。例如,如将在图11a中显示,处理Wiki图表的平均时间需要大约47秒。由于微博图表中的边数约为Wiki图表的440倍,我们将计算微博图表的处理时间大约为21千秒。这个时间消耗没有考虑到预处理,因为所有输入图表都满足介绍和第6.2节中提到的假设。对于不满足输入假设的巨大图表,根据表5,通过简单计算,一个包含443亿边的巨大图表的预处理时间将与图表的划分时间几乎相同。
6.5. Batch大小和线程数对准流模型中分区质量的影响(The Impact of Batch Size and The Number of Threads on the Partitioning Quality within the Quasi-Streaming Model)
接下来,我们将展示Batch大小$B$和并发运行的划分线程数量如何影响策略的性能。在以下实验中使用的图表是LJ、Wiki、UK和Hollywood。
6.5.1 Batch大小的影响
我们现在来评估批次大小$B$的影响。我们将分割数量固定为32。所有竞争策略的参数设置与第6.4节采用的配置相同。划分线程的数量为60,与默认设置相同。我们只改变$B$,从640增加到6400。为了全面评估影响,我们将说明批次大小B如何影响复制因子,边负载的$\sigma$值和运行时间。$B$对复制因子、边负载$\sigma$值和运行时间的影响分别在图9、10和11中说明。
首先,如图9所示,除随机策略外,所有六种策略的复制因子都随着$B$的增加而减少。另一方面,图10显示,随着$B$的增加,除DBH和随机策略外,所有六种策略的$\sigma$值都大幅下降。最后,如图11所示,所有六种策略的运行时间几乎保持不变。
现在我们分析这些结果背后的原因。对于$B$对复制因子的影响,除随机策略外,所有五种策略在$B$增加时可以获得更多信息。更多的信息将帮助这些策略做出更好的决策。注意,无论$B$大小如何,随机策略始终在所有分区中以等概率选择一个分区。因此,批次大小B对随机策略在复制因子度量和s度量两方面几乎没有影响。由于DBH通过散列更高度顶点的ID为每条边选择一个分区,所以更大的$B$几乎对DBH的$\sigma$值没有影响。另一方面,DBH是一种基于度的分区策略,可以通过尽可能地切割高度顶点来降低复制因子。因此,对于更大的$B$,顶点的部分度信息[18]更接近真实情况,这可以帮助DBH降低复制因子。
6.5.2 线程数量的影响
为了评估划分线程数量对Mint策略的影响,我们采用Mint的默认参数设置,并仅在系统模型中将线程数量从5更改为60。为了量化并行性的优势,我们将运行时间的比率定义为加速度。运行时间包括I/O时间和划分时间。Mint算法在真实世界图形上的加速度在图12中展示。如图所示,对于从分区数量k = 32到分区数量k = 64的情况,加速度几乎与划分线程数量线性相关。对于其他情况,即,分区数量在4到16之间,加速度并不线性增加。例如,在好莱坞图(图12c)上,当相应的划分线程数量分别等于15、30、40时,Mint策略可以获得其在分区数量k = 4、k = 8和k = 16时的最大加速度。在各自的点之后,加速度并不会随着更多的划分线程而增加。与线程总数相比,当分区数量相对较小时,每轮的时间成本也相对较小(参见算法2)。因此,每个批次的划分任务可以快速完成。当系统模型中的Reader线程的供给无法跟上划分线程的处理(详情参见图2)时,可能经常发生竞争条件,这对底层操作系统是一个重负。因此,当发生严重的竞争条件时,总运行时间可能会增加。
7. 结论
在这篇论文中,我们提出了一种面向边分区问题的准流式模型,并基于博弈论提出了一种相应的新颖分区策略。在准流式模型中,边流被切分为一系列批次,其中每个批次的大小是分区数的常数倍。与流式模型相比,尽管每个边可以完全了解同一批次内的边,但每个边的决策无法从批次外的其他边的决策中受益。因此,在准流式模型中执行高效的图分区可能比流式模型和离线模型更难。我们通过数学证明了游戏过程总是可以收敛到纳什平衡。然后,我们通过PoA度量这些纳什平衡的质量。实验结果表明,我们的解决方案在负载平衡指标和复制因子指标方面均优于其他五种现有的流式分区策略,无论是在真实世界的图还是随机图上。具体来说,我们基于博弈论的解决方案可以在与HDRF策略比较时,平均实现19.3%的复制因子减少和14.8倍的负载平衡指标减小,HDRF策略是当前最先进的流式边分区策略。复制因子和负载平衡指标的显著减少将提高分布式图计算系统在通信成本和计算平衡方面的性能。最后,实验结果表明,基于博弈论的策略可以在准流式模型中获得与划分线程数量几乎线性相关的加速度。我们的未来工作有两个方向。首先,我们打算基于近似纳什平衡[17]开发我们的解决方案,而不是纳什平衡,这可能会大幅度减少收敛时间,同时在分区质量上有适度的损失。其次,为了评估特定应用可以从我们的分区策略中获得多少加速度,比如PageRank,我们打算将我们的分区策略应用到未来工作中的真实分布式图计算系统[10]中。