门控循环单元 (Gated Recurrent Unit, GRU)
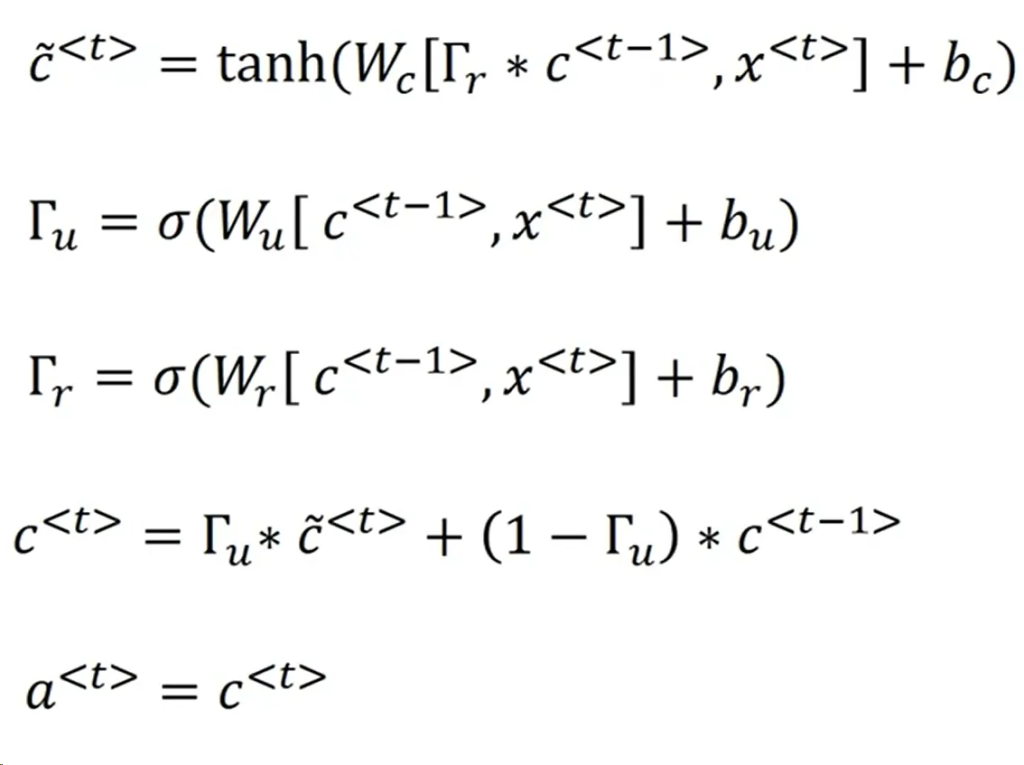
GRU是循环神经网络(RNN)中的一种变体,它具有更好的捕获长距离连接的能力,并大大帮助解决消失梯度问题。
基础RNN:
基础的RNN使用以下公式来计算在时间 t 的激活值:
$$ \begin{equation}a^t = g(W_a \times (a^{t-1}, x^t) + b)\end{equation} $$
其中,g是一个激活函数(例如tanh),$a^{t-1}$是上一时刻的激活值,$x^t$是当前时刻的输入。
GRU的原理介绍
GRU引入了一个新的变量称为“memory cell”或者记作c,它有助于网络记住关键信息(例如句子中的“cat”是单数还是复数)。在每个时间步,内存单元将有一个值 ct 。在GRU 中,输出激活值 at 实际上等于 ct。
GRU的计算方法
- Candidate Memory Cell: 首先,我们会考虑用一个值$\tilde{c}^t$来重写内存单元。这是替换$c^t$的候选值:
$$ \begin{equation}\tilde{c}^t = \tanh(W_c [c^{t-1}, x^t] + b_c)\end{equation} $$
- Update Gate: 更新门是GRU的关键部分,它决定了何时更新内存单元。更新门用符号$\Gamma_u$ 表示,并且它的值在0和1之间:
$$ \begin{equation}\Gamma_u = \sigma(W_u [a^{t-1}, x^t] + b_u)\end{equation} $$
其中,$\sigma$是sigmoid函数。
- Memory Cell Update: 使用更新门和候选内存单元,我们可以更新内存单元的实际值:
$$ \begin{equation}c^t = \Gamma_u * \tilde{c}^t + (1 – \Gamma_u) * c^{t-1}\end{equation} $$
- Relevance Gate (in Full GRU): 在完整的GRU版本中,还引入了一个相关门$\Gamma_r$,它表示$c^{t-1}$在计算下一个候选值时的相关性: $$ \begin{equation}\Gamma_r = \sigma(W_r [a^{t-1}, x^t] + b_r)\end{equation} $$
- 与此同时,候选内存单元的计算会稍微变动:
$$ \begin{equation}\tilde{c}^t = \tanh(W_c [\Gamma_r * a^{t-1}, x^t] + b_c)\end{equation} $$
通过使用更新门和相关门,GRU能更好地捕获长距离依赖关系,并帮助解决基础RNN中的消失梯度问题。