机器学习 (研究生课程)
贝叶斯分类器(Bayes Classifiers)
贝叶斯决策论(Bayesian Decision Theory)
假设有$N$种可能的类剔标记,即$Y=\{c_1,c_2,\dots,c_N\}$,$λ_{ij}$ 是将一个真实标记$c_j$样本误分类为$c_i$所产生的损失.基于后验概率$P(c_i|\vec{x})$可获得将样本$\vec{x}$分类为$c_i$所产生的期望损失( expected loss),即在样本$\vec{x}$上的”条件风险”:
$$ \begin{equation} R(c_i|\vec{x})=\sum_{j=1}^N\lambda_{ij}P(c_j|\vec{x})\end{equation} $$
总体风险:
$$ \begin{equation} R(h)=E[R(h(\vec{x})|\vec{x})]\end{equation} $$
贝叶斯判定准则(Bayes decision rule):
$$ \begin{equation} h^*(\vec{x})=\text{argmin}_{c\in Y}R(c|\vec{x})\end{equation} $$
此时,$h^*(\vec{x})$ 称之为贝叶斯最优分类器(Bayes optimal classifier),与之对应的总体风险 $R(h^*)$ 称为贝叶斯风险(Bayes risk);$1-R(h^*)$ 反映了分类器所能达到的最好性能,即通过机器学习所能产生的模型精度的理论上限。
大体来说,主要有两种策略:给定$\vec{x}$, 可通过直接建模$P(c|\vec{x})$来预测$c$,这样得到的是”判别式模型”(discriminative models);也可先对联合概率分布$P(c,\vec{x})$建模,然后由贝叶斯定理来获得$P(c|\vec{x})$, 这样得到的是”生成式模型”(generative models)。
$$ \begin{equation} P(c|\vec{x})={P(c)P(\vec{x}|c)\over P(\vec{x})} \end{equation} $$
直接根据样本出现的频率来估计类条件概率$P(\vec{x}|c)$将会遇到严重的困难(样本可能太小)。
极大似然估计(Maximum Likelihood Estimation)
估计类条件概率的一种常用策略是先假定其具有某种确定的概率分布形式,再基于训练样本对概率分布的参数进行估计。例如在连续属性情形下,假设概率密度函数$P(\vec{x}|c)\sim N(\mu_c,\sigma_c^2)$, 则参数$\mu_c$和$\sigma_c^2$的极大似然估计为:
$$ \begin{equation} \left\{\begin{array}{lr} \hat{\mu_c}={1\over |D_c|}\sum_{\vec{x}\in D_c}\vec{x} \\ \hat{\sigma_c^2}={1\over |D_c|}\sum_{\vec{x}\in D_c}(\vec{x}-\hat{\mu_c}) (\vec{x}-\hat{\mu_c})^T \end{array} \right. \end{equation} $$
朴素贝叶斯分类器(Naive Bayes classifier):
属性条件独立性假设:
$$ \begin{equation} P(c|\vec{x})={P(c)P(\vec{x}|c)\over P(\vec{x})} ={P(c)\over P(\vec{x})}\prod_{i=1}^dP(\vec{x_i}|c) \end{equation} $$
由于对所有类别来说$P(\vec{x})$相同,因此贝叶斯判定准则有:
$$ \begin{equation} h_{nb}(\vec{x})=\text{argmax}_{c\in Y}P(c)\prod_{i=1}^dP(\vec{x_i}|c)\end{equation} $$
显然,朴素贝叶斯分类器的训练过程就是基于训练集D 来估计类先验概率$P(c)$,并为每个属性估计条件概率$P(\vec{x_i}|c)$;因此,对于离散属性而言,可以直接利用频率估计概率:
$$ \begin{equation} P(\vec{x_i}|c)={|D_{c,\vec{x_i}}|\over |D_{c}| } \end{equation} $$
连续属性可考虑概率密度函数,假定$P(\vec{x_i}|c)=N(\mu_{c,i},\sigma_{c,i}^2)$,然后使用(5)参数估计方法。半朴素贝叶斯分类器(Semi-Naive Bayes classifier):
假设每个属性在类别之外最多仅依赖于一个其他属性:
$$ \begin{equation} P(c|\vec{x})\propto P(c)\prod_{i=1}^dP(\vec{x_i}|(c,pa_i)) \end{equation} $$
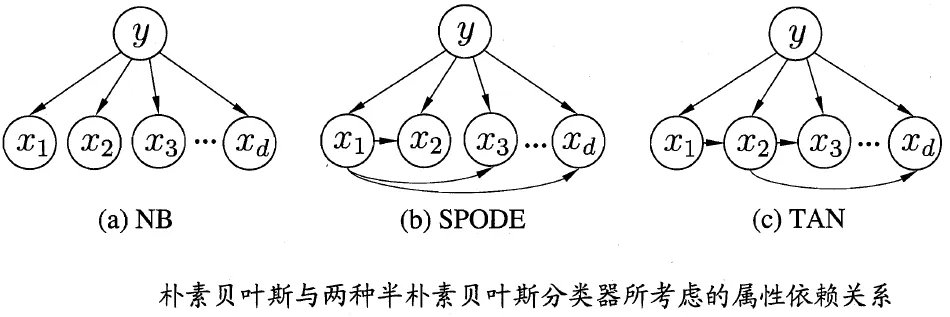
贝叶斯网络(Bayesian Network)

属性$\{\vec{x_1}, \vec{x_2},\dots,\vec{x_d}\}$(依赖于属性$\{\vec{\pi_1}, \vec{\pi_2},\dots,\vec{\pi_d}\}$)的联合概率分布定义为:
$$ \begin{equation} P({\vec{x_1}, \vec{x_2},\dots,\vec{x_d}})=\prod_{i=1}^dP_B(\vec{x_i}|\vec{\pi_i}) \end{equation} $$
以上图为例,联合概率分布定义为:
$$ \begin{equation} P(\vec{x_1},\vec{x_2},\vec{x_3},\vec{x_4},\vec{x_5})=P(\vec{x_1}) P(\vec{x_2})P(\vec{x_3}|\vec{x_1})P(\vec{x_4}|(\vec{x_1},\vec{x_2})) )P(\vec{x_5}|\vec{x_2}) \end{equation} $$
贝叶斯网中三个变量之间的典型依赖关系:
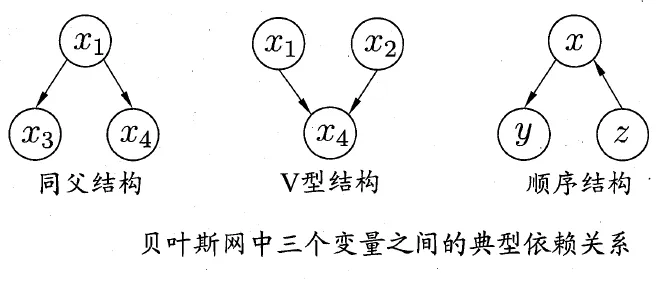
从贝叶斯网络(Bayesian Network)到道德图(Moral Graph):
- 找出有向图中的所有V型结构,在V型结构的两个父结点之间加上一条无向边;
- 将所有有向边改为无向边。
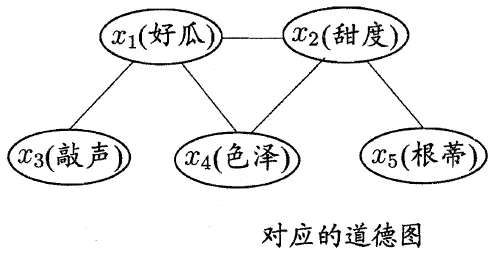
所有条件独立夫系:$\vec{x_3}\perp\vec{x_4}|\vec{x_1}$,$\vec{x_4}\perp\vec{x_5}|\vec{x_2}$,$\vec{x_3}\perp\vec{x_2}|\vec{x_1}$,$\vec{x_3}\perp\vec{x_5}|\vec{x_1}$,$\vec{x_3}\perp\vec{x_5}|\vec{x_2}$等
集成学习(Ensemble Learning)
根据个体学习器的生成方式,目前的集成学习方法大致可分为两大类,即个体学习器问存在强依赖关系、必须串行生成的序列化方法,以及个体学习器间不存在强依赖关系、可同时生成的并行化方法;前者的代表是Boosting ,后者的代表是Bagging 和”随机森林” (Random Forest)。
自适应增强(Adaptive Boosting, AdaBoost)
AdaBoost是一种常用的Boosting算法。它通过调整训练样本的权重来改进每个后续弱学习器的性能。首先,所有训练样本的权重被设置为相等。在每轮训练中,根据上一轮学习器的错误率来更新采样权重。预测错误的样本权重会增加,预测正确的样本权重会减少。这样,在后续的训练中,学习器会更加关注之前预测错误的样本,从而改进整体性能。
算法过程:
- 初始化:输入参数为训练集$D=\{(\vec{x_1},y_1),(\vec{x_2},y_2),\dots,(\vec{x_m},y_m)\}$,循环总次数$k_{\max}$,采样权重$W_k(i)={1\over n},i=1,2,\dots,m$;
- $k=0$;$k = k+1$;
- 使用采样权重$W_k(i)$采样训练集$D$对弱学习器$C_k$进行训练;
- 基于训练结果的错误率。计算弱学习器的系数$\epsilon_k={1\over 2}\times \ln({1-error\_rate \over error\_rate})$;
- 计算$\alpha_k={1\over2}\ln({1-\epsilon_k\over \epsilon_k})$,用于根据学习器对样本的预测结果更新采样权重;
- $W_{k+1}(i)\leftarrow W_k(i) \times \left\{\begin{array}{lr} e^{-\alpha_k}, \text{if}\space h_k(\vec{x_i})=y \\e^{\alpha_k} ,\space\space\text{if}\space h_k(\vec{x_i})\neq y \end{array} \right. \text{for}\space i=1,2,\dots,m$;
- $W_{k+1}$归一化;
- 当$k\neq k_{\max}$返回第三步,否则继续执行下一步;
- 返回结果$C_k$和$\alpha_k$,$k=1,2,\dots,k_{\max}$,结束。
训练完成后,根据每个弱学习器的系数对它们进行加权组合,形成最终的强学习器。对于二分类问题,可以使用加权多数投票的方式进行预测:对于一个新的输入样本,计算各个弱学习器加权预测值的和,然后根据和的正负判断该样本属于哪个类别。
AdaBoost算法的优点在于它能够自适应地调整训练样本的权重,使得在每一轮训练中,弱学习器都关注之前预测错误的样本。通过逐步组合这些弱学习器,AdaBoost能够实现较高的预测性能。然而,这种串行训练过程可能导致较慢的训练速度,对于存在噪声数据的情况,AdaBoost可能会过拟合。
引导聚集(Bootstrap AGGregatING, Bagging)算法
给定一个大小为$n$的训练集 $D$,从中均匀、有放回地(自助抽样法)选出$m$个大小为$n’$的子集 $D_i$ 作为新的训练集。在这$m$个训练集上使用分类、回归等算法,则可得到$m$个模型,再通过取平均值、投票等方法,可得到Bagging的结果;例如如果使用投票的方法:
$$ \begin{equation} H(\vec{x})=\text{argmax}_{y\in Y}\sum_{t=1}^T1(h_t(\vec{x})=y) \end{equation} $$
包外预测:
$$ \begin{equation} H^{oob}(\vec{x})=\text{argmax}_{y\in Y}\sum_{t=1}^T{1(h_t(\vec{x})=y) \times 1(\vec{x} \notin D_t)} \end{equation} $$
泛化误差的包外估计:
$$ \begin{equation} \epsilon^{oob}={{1\over |D|} \sum_{(\vec{x},y)\in D }1(H^{oob}(\vec{x})\neq y)} \end{equation} $$
随机森林(Random Forest, RF)
RF在以决策树为基学习器构建 Bagging 集成的基础上,在决策树的训练过程中引入了随机属性选择。具体来说,传统决策树在选择划分属性时是在当前结点的属性集合(假定有$d$个属性)中选择一个最优属性;而在RF中,对基决策树的每个结点,先从该结点的属性集合中随机选择一个包含$k$个属性的子集,然后再从这个子集中选择一个最优属性用于划分。这里的参数$k$控制了随机性的引入程度;若令$k=d$ ,则基决策树的构建与传统决策树相同;若令 $k=1$, 则是随机选择一个属性用于划分; 一般情况下,推荐值$k=log_2d$。
结合策略
平均法(回归任务,连续输出):
- 简单平均分:$H(\vec{x})={1\over T}\sum_{i=1}^Th_i(\vec{x})$;
- 加权平均法:$H(\vec{x})={1\over T}\sum_{i=1}^Tw_ih_i(\vec{x}),w_i\geq0,\sum_{i=1}^Tw_i=1$。
投票法(分类任务,你上输出):
假设学习器$h_i$在类别标记集合$\{c_1,c_2,\dots,c_N\}$预测一个标记类别(Multi-Class),在样本$\vec{x}$上的预测输出表示为一个$N$维向量$(h_i^1(i),h_i^2(i),\dots,h_i^N(i))$:
- 绝对多数投票:
$$ \begin{equation} H=\begin{cases} c_j&\quad \text{if} \space\sum_{i=1}^Th_i^j(\vec{x})\gt {1\over2}\sum_{k=1}^N\sum_{i=1}^Th_i^k(\vec{x})\\ reject&\quad \text{otherwise}\end{cases}\end{equation} $$
- 相对多数投票
- 加权投票:硬投票、软投票
学习法:
- Stacking:
Stacking 首先从初始数据集训练出初级学习器,然后生成一个新数据集用于训练次级学习器。在这个新数据集中,初级学习器的输出当作样例输入特征,初始样本的标记被当作样例标记。
多样性
集成的”分歧”表示个体学习器在样本$\vec{x}$上的不一致性:
$$ \begin{equation}\bar{A}(h|\vec{x})=\sum_{i=1}^Tw_iA(h_i|\vec{x})=\sum_{i=1}^Tw_i(h_i(\vec{x})-H(\vec{x}))^2\end{equation} $$
个体学习器准确性越高、多样性越大,则集成越好。
多样性度量(diversity measure)用于度量集成中个体分类器的多样性,即估算个体学习器的多样化程度.典型做法是考虑个体分类器的两两相似、不相似性。
对二分类任务, $y\in\{-1,+1\}$,分类器$h_i$与$h_j$的预测结果列联表(contingency table):
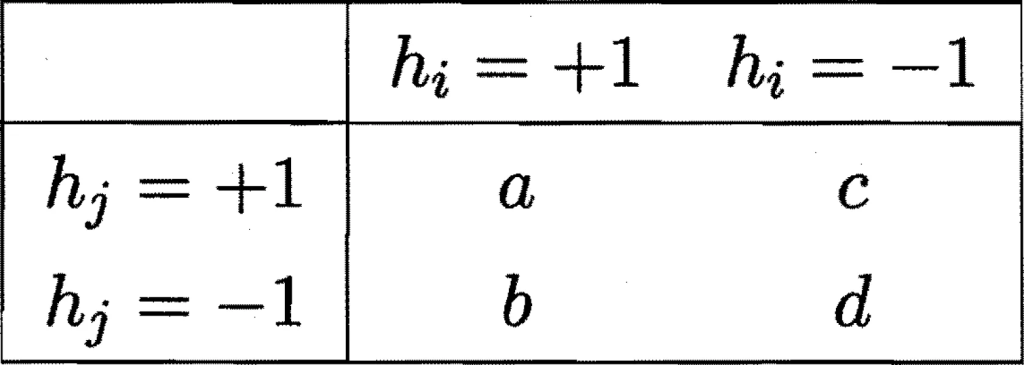
- 不合度量(disagreement measure),值越大则多样性越太:
$$ \begin{equation} dis_{ij}={b+c\over m} \in[0,1] \end{equation} $$
- 相关系数(correlation coefficient),值为0无关,否则表示正/负相关:
$$ \begin{equation} \rho_{ij}={ad-bc\over \sqrt{(a+b)(a+c)(c+d)(b+d)}} \in [-1,+1]\end{equation} $$
- Q-绩计量(Q-statistic ),$|Q_{ij}|\leq|\rho_{ij}|$:
$$ \begin{equation} Q_{ij}={ad-bc\over ad+bc} \in [-1,+1]\end{equation} $$
- $\kappa$-统计量($\kappa$-statistic):
$$ \begin{equation} \kappa={{a+d\over m} +{(a+b)(a+c)+(c+d)(b+d)\over m^2}\over 1-{(a+b)(a+c)+(c+d)(b+d)\over m^2}}\end{equation} $$
若分类器$h_i$与$h_j$在$D$上完全一致,则$\kappa=1$;若它们仅是偶然达成一致,则$\kappa=0$;
并且$\kappa$ 通常为非负值,仅在$h_i$ 与$h_j$达成一致的概率甚至低于偶然性的情况下取负值。