神经网络 (Neural Network)
简单神经网络示例
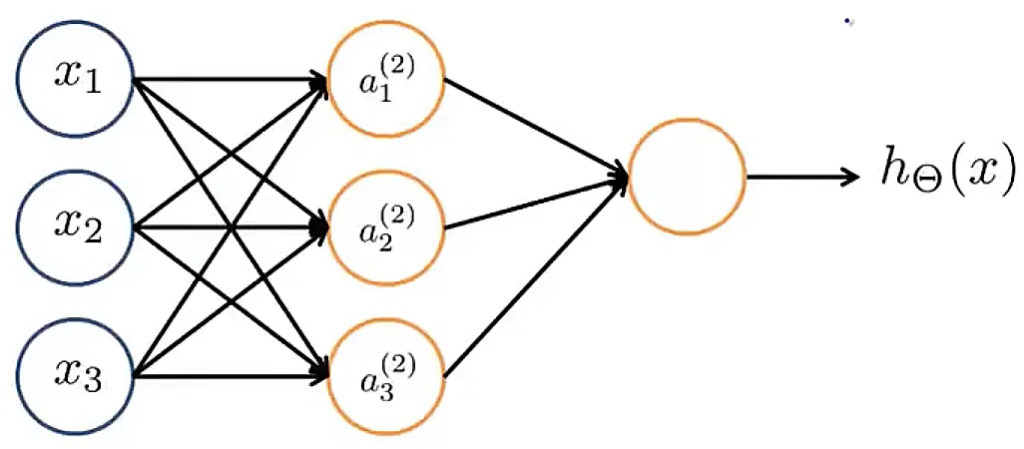
$$ \begin{equation} \left\{\begin{array}{lr}a_1^{(2)}=g(\Theta_{1,0}^{(1)}+\Theta_{1,1}^{(1)}x_1+\Theta_{1,2}^{(1)}x_2+\Theta_{1,3}^{(1)}x_3) \\ a_2^{(2)}=g(\Theta_{2,0}^{(1)}+\Theta_{2,1}^{(1)}x_1+\Theta_{2,2}^{(1)}x_2+\Theta_{2,3}^{(1)}x_3) \\ a_3^{(2)}=g(\Theta_{3,0}^{(1)}+\Theta_{3,1}^{(1)}x_1+\Theta_{3,2}^{(1)}x_2+\Theta_{3,3}^{(1)}x_3) \\ h_{\Theta}(x)=a_1^{(3)}=g(\Theta_{1,0}^{(2)}+\Theta_{1,1}^{(2)}a_1^{(2)}+\Theta_{1,2}^{(1)}a_2^{(2)}+\Theta_{1,3}^{(2)}a_3^{(2)}) \end{array}
\right.\end{equation} $$
其中$g(z)={1\over{1+e^{-z}}}$. 神经元经过激活函数后,其值$a^{(i)}_j \in (0,1)$.
If networks has $s_j$ units in layer j, $s_{j+1}$ units in layer j+1, then $\Theta^{(j)}$ will be of dimensions $s_{j+1} \times (s_{j} + 1)$
多元分类(Multiple output units: One-vs-all)网络示例
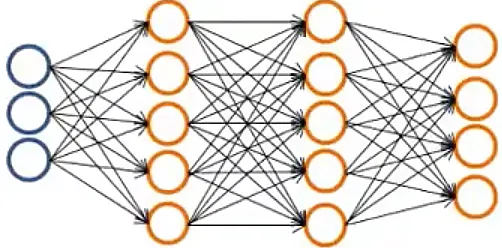
$h_\Theta(x) \in (0, 1)^4$; want $h_\Theta(x) \approx \begin{bmatrix} 1 \\ 0 \\ 0 \\ 0
\end{bmatrix}$when pedestrain, $h_\Theta(x) \approx \begin{bmatrix} 0 \\ 1 \\ 0 \\ 0
\end{bmatrix}$when car, $h_\Theta(x) \approx \begin{bmatrix} 0\\ 0 \\ 1 \\ 0
\end{bmatrix}$when motorcycle, $h_\Theta(x) \approx \begin{bmatrix} 0 \\ 0 \\ 0 \\ 1
\end{bmatrix}$when truck.
Cost Function
$h_\Theta(x) \in (0, 1)^K$and $h_\Theta(x) \approx \begin{bmatrix} [h_\Theta(x)]1 \\ [h\Theta(x)]2 \\ \vdots \\ [h\Theta(x)]_K
\end{bmatrix}$, as well as L layers with $s_l$ units at $l$ layer, so
$$ \begin{equation}\begin{split}J(\Theta)=-{1\over m}\sum_{i=1}^m\sum_{k=1}^K{(y^{(i)}log([h_\theta(x^{(i)})]k)+(1-y^{(i)})log(1-[h\theta(x^{(i)})]k))}\\ + {\lambda \over 2m}\sum{l=1}^{L-1}\sum_{j=1}^{s_{l}}\sum_{i=1}^{s_{l+1}}(\Theta_{i,j}^{(l)})^2\end{split}\end{equation} $$
反向传播(Back Propogation)
$\delta_j^{(l)}$ is the “error” of node $j$ at layer $l$, note $a^{(i)}_0 = 1, i=2,3,\cdots,L-1$ aren’t considered:
$$ \begin{equation} \left\{\begin{array}{lr} \delta^{(L)} = a^{(L)} – y \\ \delta^{(L-1)} = (\Theta^{(L-1)})^T\delta^{(L)} .* (a^{(L-1)} .* (1-a^{(L-1)})) \\ \delta^{(L-2)} = (\Theta^{(L-2)})^T\delta^{(L-1)} .* (a^{(L-2)} .* (1-a^{(L-2)})) \\ \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \space \vdots \\ \delta^{(2)} = (\Theta^{(2)})^T\delta^{(3)} .* (a^{(2)} .* (1-a^{(2)})) \end{array}
\right.\end{equation} $$
$\delta_i^{(l)}$表示第 $l$ 层第 $i$ 个神经元的误差;由于第1层作为输入层、$a^{(i)}_0$并不存在误差因此不需计算$\delta$.
吴恩达机器学习视频–神经网络反向传播算法公式推导_xuan_liu123的博客-CSDN博客_神经网络反向传播公式
未验证的证明过程,收藏以供参考
算法过程
下为反向传播迭代一次的过程,其中${\partial J(\Theta) \over \partial \Theta_{ij}^{(l)}} = D_{ij}^{(l)}$:
Training set $\{(x^{(1)},y^{(1)}), (x^{(2)},y^{(2)})\},\cdots,(x^{(m)},y^{(m)}) \}$
Set $\Delta_{ij}^{(l)} = 0$ for all $l$, $i$, $j$
For $i=1$ to $m$
$\space\space\space\space$Set $a^{(1)}=x^{(i)}$
$\space\space\space\space$Perform forward propagation to compute $a^{(l)}$ for $l=2,3,\\cdots,L$
$\space\space\space\space$Using $y^{(i)}$ to compute $\\delta^{(L)}=a^{(L)}-y^{(i)}$
$\space\space\space\space$Compute $\\delta^{(L-1)},\\delta^{(L-2)},\\cdots,\\delta^{(2)}$
$\space\space\space\space$$\\Delta_{ij}^{(l)} := \\Delta_{ij}^{(l)} + a_j^{(l)}\\delta^{(l+1)}_i$ for all $l$, $i$, $j$
$D_{ij}^{(l)} := {1\over m}\Delta_{ij}^{(l)} + \lambda\Theta_{ij}^{(l)}$ if $j \neq 0$
$D_{ij}^{(l)} := {1\over m}\Delta_{ij}^{(l)}$ if $j = 0$
梯度检测
随机初始化
- Don’t use zero initialization
- Initial $\Theta_{ij}^{(l)}$ to a random value in $[-\epsilon, \epsilon]$
训练神经网络
- 输入层神经元数量:Dimension of features
- 输出单位数量:Number of classes
- 合理的默认值:1个隐藏层,或者>1个隐藏层,则在每一层中具有相同数量的隐藏单元