并行图相似性计算的基础知识 (Basic Knowledge for Paralleled Graph Similarity)
在数据结构中,图的相似性度量主要用于比较两个或多个图的拓扑结构或属性相似程度。
- 图同构(Graph Isomorphism): 图同构用于判断两个图是否具有相同的拓扑结构,即它们的节点和边是否可以一一对应。如果两个图是同构的,那么它们具有最高的相似性。
- 子图同构(Subgraph Isomorphism): 子图同构比较两个图之间是否存在相似的子图结构。这可以用于在一个大图中查找特定的图模式。
- 最大公共子图(Maximum Common Subgraph, MCS): 最大公共子图是指两个图之间具有最大相似节点和边的子图。通过计算最大公共子图的大小,可以评估两个图之间的相似程度。
- 图编辑距离(Graph Edit Distance, GED): 图编辑距离是衡量两个图相似性的一种方法,通过计算将一个图转换为另一个图所需的最少编辑操作数(如添加、删除或重命名节点和边)来度量相似性。
- 节点和边的属性相似性(Node and Edge Attribute Similarity): 在具有属性的图中,可以通过比较节点和边的属性值(例如权重、颜色等)来度量图之间的相似性。
- 谱方法(Spectral Methods): 谱方法通过比较图的谱属性(例如邻接矩阵或拉普拉斯矩阵的特征值和特征向量)来度量图之间的相似性。谱方法通常用于网络嵌入和聚类任务。
- 图核方法(Graph Kernel Methods): 图核方法通过定义一个核函数来度量两个图之间的相似性。核函数可以将图映射到高维特征空间,然后在这个空间中计算图之间的相似性。常见的图核方法包括随机游走核、最短路径核和子图核等。
- 网络嵌入方法(Network Embedding Methods): 网络嵌入方法通过将图中的节点或子图映射到低维向量空间来度量图之间的相似性。这种方法通常用于图分类和链接预测任务。常见的网络嵌入方法包括DeepWalk、Node2Vec和GraphSAGE等。
这些方法可以根据具体问题和应用场景进行选择和组合。在实际应用中,可能需要考虑图的规模、密度、属性等因素来确定最合适的相似性度量方法。
图同构(Graph Isomorphism)
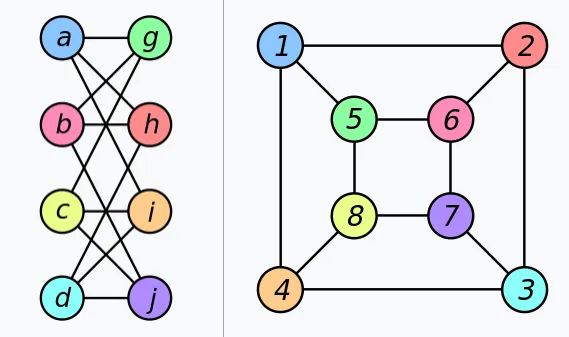
只有节点数目相同的两个图才有可能同构。两简单图$G$和$H$称为是同构,当且仅当存在一个将$G$中的节点$1,2,…,n$映射到$H$中的节点$1,2,…,n$的一一对应$\sigma$,使得$G$中的任意两节点$i$和$j$相连接,当且仅当$H$中对应的两个节点$\sigma(i)$和$\sigma(j)$相连接,同构可记作$G\cong H$.
子图同构(Subgraph Isomorphism)
给定图⁍和⁍,图⁍中的节点数目小于⁍,问是否存在⁍的某一子图(subgraph),与⁍同构?
最大公共子图(Maximum Common Subgraph, MCS)
最大公共子图(Maximum Common Subgraph, MCS)问题是寻找两个图之间具有最大相似节点和边的子图。MCS问题是一个NP-hard问题,因此没有已知的多项式时间算法来解决它。
可以将最大公共子图问题最大团(Maximum Clique)问题:
$G$和$H$的模积(modular product)的顶点集是笛卡尔积$V(G)×V(H)$,任意两顶点$(u, v)$和$(u’ , v’ )$ 在$G$和$H$的模积中相邻当且仅当$u$不同于$u’$,$v$不同于$v’$,并且:
- u is adjacent with u’ and v is adjacent with v’ , or
- u is not adjacent with u’ and v is not adjacent with v’ .
模积图中的团(cliques)对应于$G$和$H$的生成子图中的同构(isomorphisms)。、
因此,模积图可用于将生成子图中的同构(包括最大公共子图问题)简化为图中寻找团问题。
图编辑距离(Graph Edit Distance, GED)
编辑操作
标准的编辑操作有6种,即点或边的删除、插入和替换。假设存在点$u$,$v$和空点$\epsilon$,则$u$的删除操作表示为$(u\rightarrow\epsilon)$,点$v$的插入操作表示为$(\epsilon\rightarrow v)$,点$u$替换为点$v$表示为$(u\rightarrow v)$;边的3种操作的表示方法与此类似。
编辑路径
将图$g_1$转化成图$g_2$所需的一系列编辑操作的序列集合记为$k$,$e_i$ 表示第$i$步编辑操作,$k=(e_1,…,e_i,…,e_n)$,则称$k$为图$g_1$和$g_2$ 间的完全编辑路径。
节点和边的属性相似性(Node & Edge Attribute Similarity)
在具有属性的图中,可以通过比较节点和边的属性值(例如权重、颜色等)来度量图间相似性。