自注意力机制 (Self-Attention)
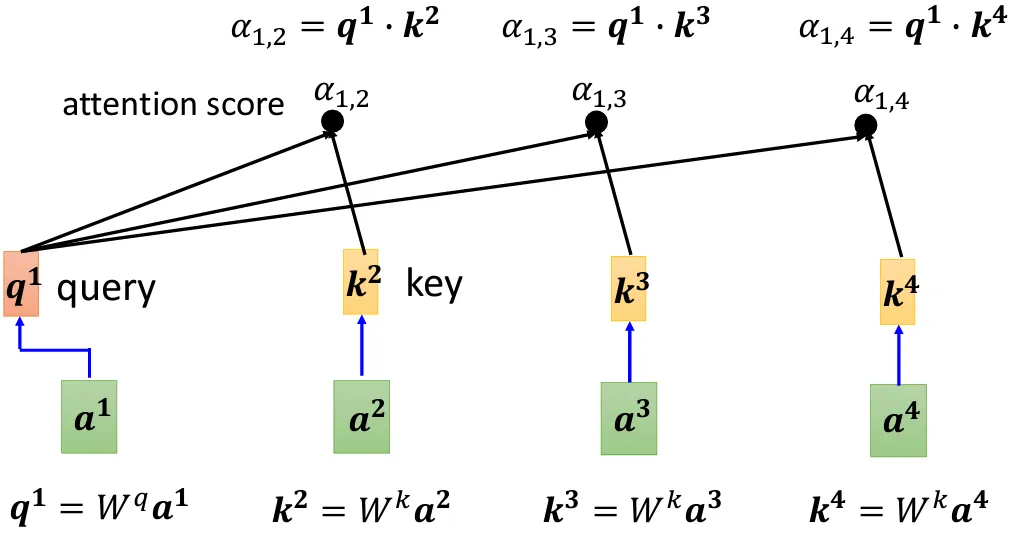
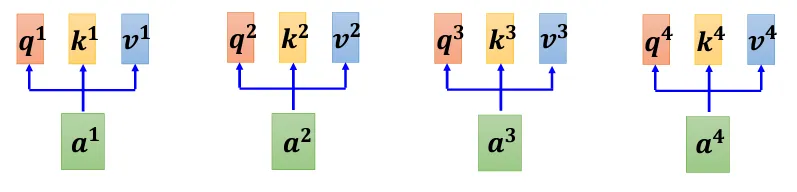
- $\boldsymbol{a^1}$、$\boldsymbol{a^2}$、$\boldsymbol{a^3}$和$\boldsymbol{a^4}$分别表示 Self-Attention 输入
- $W^q$、$W^k$和$W^v$用于生成输入的$\boldsymbol{q}$、$\boldsymbol{k}$和$\boldsymbol{v}$向量
- 在上图中,例如$\alpha_{m,n}$ 表示$\boldsymbol{a^m}$和$\boldsymbol{a^n}$的关联分数
$$ \begin{equation}\alpha^{i,j}=q^i\times k^j\end{equation} $$
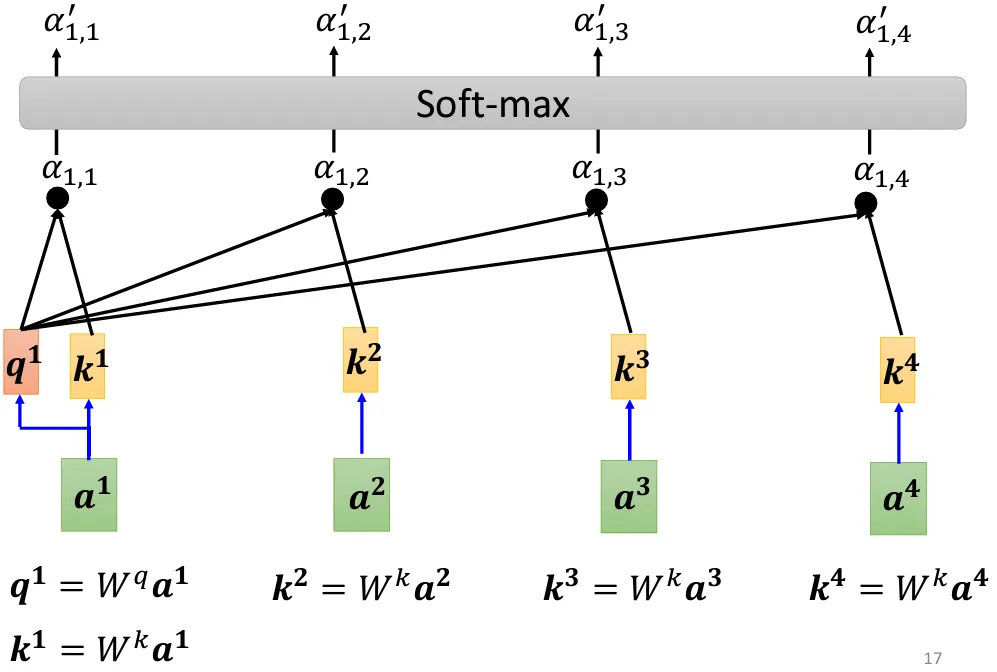
- 一般而言,也需要计算 $\boldsymbol{a^m}$ 和其自身的关联性分数
- 同时在最后一般给所有关联性分数套一个Soft-max
- 至此,我们已经解释$\boldsymbol{q}$和$\boldsymbol{k}$向量的作用,还有$\boldsymbol{v}$向量
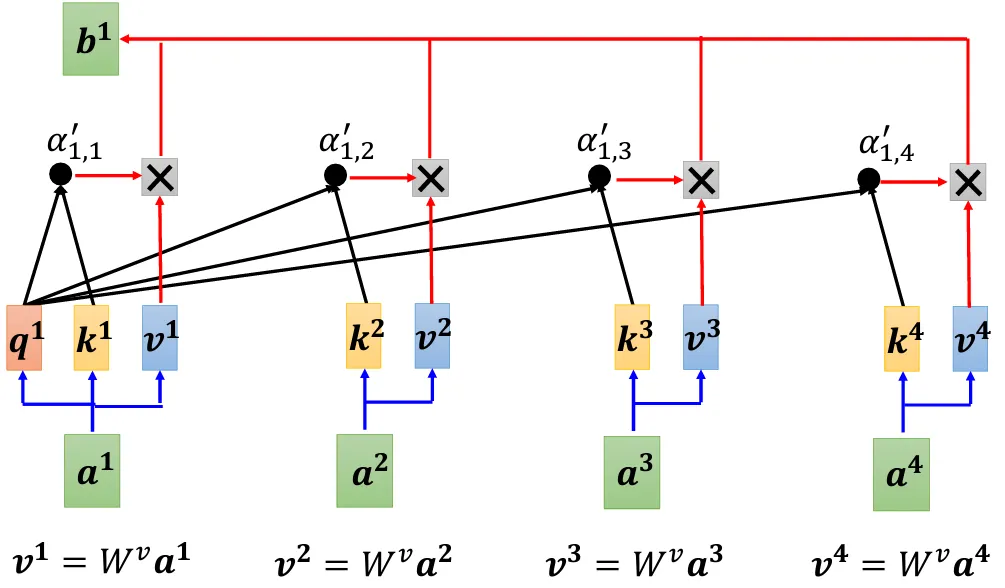
- $\boldsymbol{v^m}$ 作用是从与向量 $\boldsymbol{a^m}$ 相关的关联性分数中提出信息
- 例如如果某个$\alpha^{‘}_{1,i}$值越大,最后$\boldsymbol{b^1}$向量与其相关性越强
- Extract information based on attention scroes:
$$ \begin{equation}\boldsymbol{b^1}=\sum_{i}{a^{‘}_{1,i}}\boldsymbol{v^i}\end{equation} $$
$$\begin{equation}\left\{\begin{array}{lr}Q=W^q\times I\\\\K=W^k\times I\\\\V=W^v\times I\end{array} \right.\end{equation} $$
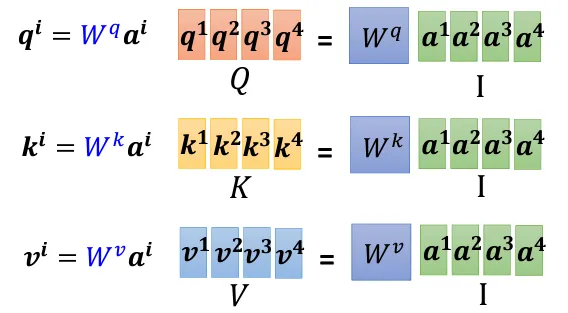
- 上图演示 Self-Attention中的$Q$、$K$和$V$矩阵是如何得到的
- 值得注意的是,$W^q$、$W^k$和$W^v$矩阵是需要被训练得到的

- 使用分块矩阵理解上面的矩阵乘法
$$ \begin{equation}\left\{\begin{array}{lr}A=K^T\times Q \\\\A’=\text{softmax}(A)\\\\O=V\times A’\end{array} \right.\end{equation} $$
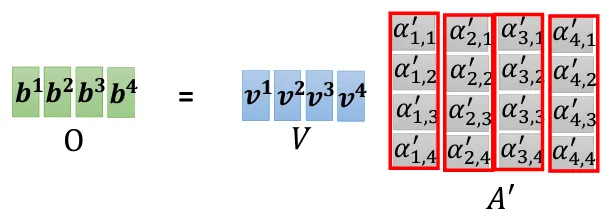
- $I$和$O$分别表示 Seft-attention 的输入和输出
Multi-head Self-Attention
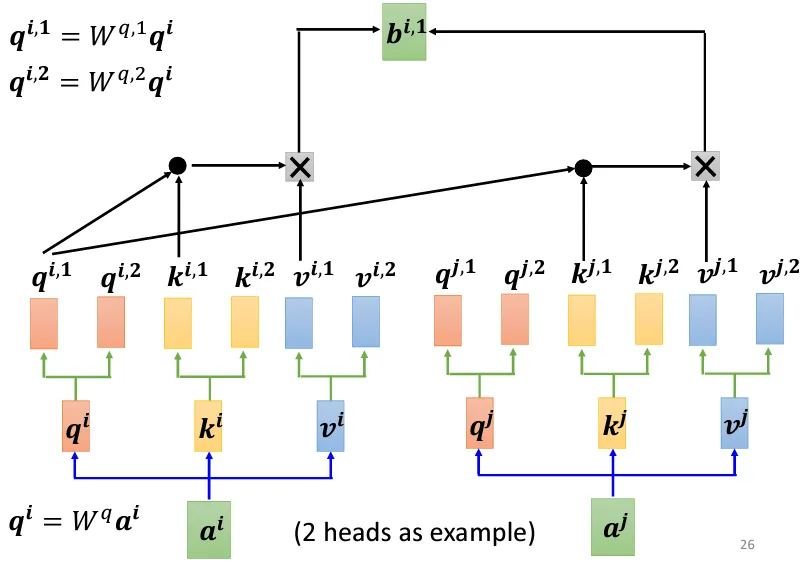
- 首先依然有:
$$ \begin{equation}\left\{\begin{array}{lr}q^i=W^q\times a^i \\k^i=W^k\times a^i\\v^i=W^v\times a^i\end{array} \right.\end{equation} $$
- 如果有$h$个head,那么也有:
$$ \begin{equation}\left\{\begin{array}{lr}q^{i,1}=W^{q,1}\times q^i \\q^{i,2}=W^{q,2}\times q^i \\\qquad\vdots\\q^{i,h}=W^{q,h}\times q^i \\k^{i,1}=W^{k,1}\times k^i \\k^{i,2}=W^{k,2}\times k^i \\\qquad\vdots\\k^{i,h}=W^{k,h}\times k^i \\v^{i,1}=W^{v,1}\times v^i \\v^{i,2}=W^{v,2}\times v^i \\\qquad\vdots\\v^{i,h}=W^{v,h}\times v^i \end{array} \right.\end{equation} $$
$$ \begin{equation}\left\{\begin{array}{lr}\alpha_{i,j,1}=q^{i,1}\times k^{j,1}\\\alpha_{i,j,2}=q^{i,2}\times k^{j,2}\\\ \ \qquad\vdots\\\alpha_{i,j,h}=q^{i,h}\times k^{j,h}\end{array} \right.\end{equation} $$

$$ \begin{equation}\boldsymbol{b^{i,k}}=\sum_{j}{a^{‘}_{i,j,k}}\boldsymbol{v^{j,k}}\end{equation} $$
- 最后multi-head经由$W^O$回到single-head